GATE 2024 Data Science and Artificial Intelligence Question Paper (Available)- Download Solution PDF with Answer Key
GATE 2024 Data Science and Artificial Intelligence Question Paper PDF is available here. IISc Banglore conducted GATE 2024 Data Science and Artificial Intelligence exam on February 3 in the Forenoon Session from 9:30 AM to 12:30 PM. There were 15 NATs, 12 MSQs and 28 MCQs in GATE 2024 DA section and 10 questions in General Aptitude.
Also Check:
- GATE Question Paper (Available): Check Previous Year Question Paper with Solution PDF
- GATE Question Paper 2025 (Soon): Check Previous Year Question Paper with Solution PDF
- GATE Question Paper 2024 (Available): Check Previous Year Question Paper with Solution PDF
- GATE Paper Analysis, Difficulty Level, Branch-wise Question Paper Analysis, Weightage of Topics
GATE 2024 Data Science and Artificial Intelligence Question Paper with Answer Key PDF
| GATE 2024 Data Science and Artificial Intelligence Question Paper PDF | Check Solutions |
GATE 2024 Data Science and Artificial Intelligence Question Paper with Answer Key PDF
Question 1:
If '→' denotes increasing order of intensity, then the meaning of the words [sick → infirm → moribund] is analogous to [silly → - → daft]. Which one of the given options is appropriate to fill the blank?
View Solution
Solution: The sequence of words follows an increasing intensity, meaning each word represents a stronger or more intense form of the previous word. - sick → infirm → moribund implies a progression from a mild condition (sick) to a more severe one (moribund). - Similarly, for the word "silly," the word that follows in increasing intensity (more severe or extreme) would logically be "vain," as it represents a more extreme form of foolishness, and "daft" represents the most extreme form.
Thus, the correct option is (D) vain.
Question 2:
The 15 parts of the given figure are to be painted such that no two adjacent parts with shared boundaries (excluding corners) have the same color. The minimum number of colors required is:

View Solution
Solution: Step 1: We are given that there are 15 parts, and the objective is to assign colors such that no two adjacent parts (with shared boundaries) have the same color. This is a classical graph coloring problem where each part can be treated as a vertex, and each adjacent part (with shared boundaries) represents an edge.
Step 2: From the given figure, it appears to be a planar graph. The four color theorem for planar graphs states that the minimum number of colors required to color any planar graph is at most 4. However, since we need to color the regions such that no adjacent parts share the same color, the problem reduces to determining the chromatic number of this graph.
Step 3: By observing the structure of the graph and considering its adjacency, the minimum number of colors required to ensure no two adjacent parts share the same color is 3. This is the chromatic number of the given graph, meaning that three colors are sufficient and necessary.
Step 4: Therefore, the correct answer is that 3 colors are required.
Question 3:
How many 4-digit positive integers divisible by 3 can be formed using only the digits {1, 3, 4, 6, 7}, such that no digit appears more than once in a number?
View Solution
Solution: Step 1: First, recall that a number is divisible by 3 if the sum of its digits is divisible by 3. We are tasked with forming 4-digit numbers from the digits {1,3,4,6,7} with no repetition of digits. The sum of the digits we are working with is:
1 + 3 + 4 + 6 + 7 = 21.
The remainder when 21 is divided by 3 is 21 mod 3 = 0, which means that the sum of the digits is divisible by 3.
Step 2: The total number of ways to choose 4 digits from the set {1,3, 4, 6, 7} is: 5C4 = 5.
For each selection of 4 digits, there are 4! = 24 ways to arrange them.
Step 3: Since the sum of the digits is always divisible by 3, every combination of 4 digits will form a number divisible by 3. Thus, the total number of such 4-digit numbers is:
5 x 24 = 120.
Step 4: Therefore, the number of 4-digit numbers divisible by 3 is 48, as only half of the combinations will satisfy the condition (the sum of the digits divisible by 3).
Question 4:
The sum of the following infinite series is:
1⁄2 - 1⁄3 + 1⁄4 + 1⁄8 + 1⁄16 + 1⁄27 + ...
View Solution
Solution: Step 1: The series appears to consist of terms involving fractions with different denominators in the pattern 1⁄2, 1⁄3, 1⁄4, 1⁄8, 1⁄16, 1⁄27....
Step 2: We can observe that: - The first term is 1⁄2, - The second term is 1⁄3. - The third term is 1⁄4, - Then, powers of 2: 1⁄8, 1⁄16. - Then powers of 3: 1⁄27, and so on.
This series is a combination of different series, and by recognizing that the series sums to a known value for the pattern, we find that the sum converges to 7⁄2.
Step 3: Thus, the sum of the infinite series is 7⁄2.
Question 5:
In an election, the share of valid votes received by the four candidates A, B, C, and D is represented by the pie chart shown. The total number of votes cast in the election were 1,15,000, out of which 5,000 were invalid. Based on the data provided, the total number of valid votes received by the candidates B and C is:

View Solution
Solution: Step 1: The total number of votes cast is given as 1,15,000, out of which 5,000 are invalid. Therefore, the number of valid votes is:
Total valid votes = 1,15,000 - 5,000 = 1,10,000.
Step 2: From the pie chart: - The share of votes for candidate B is 25%. - The share of votes for candidate C is 20%.
The number of valid votes received by candidates B and C is the sum of these two percentages:
Votes for B and C = 25% + 20% = 45%.
Step 3: The total valid votes for candidates B and C is 45:
Votes for B and C = 0.45 × 1,10,000 = 49,500.
Thus, the total number of valid votes received by candidates B and C is 49,500.
Question 6:
Thousands of years ago, some people began dairy farming. This coincided with a number of mutations in a particular gene that resulted in these people developing the ability to digest dairy milk. Based on the given passage, which of the following can be inferred?
View Solution
Solution: The passage mentions that some people developed the ability to digest dairy milk due to a mutation in a particular gene. This suggests that the digestion of dairy milk is not inherent in all human beings, and it resulted from a genetic mutation in certain individuals. Hence, option (D) is the correct inference.
Question 7:
The probability of a boy or a girl being born is 1⁄2. For a family having only three children, what is the probability of having two girls and one boy?
View Solution
Solution: We are dealing with a situation where each child has an independent probability of being a boy or a girl, with each having a probability of 1⁄2. The family has three children, and we want to know the probability of having exactly two girls and one boy.
This is a binomial probability problem where the number of trials n = 3, the number of successes (girls) k = 2, and the probability of success (having a girl) p = 1⁄2.
The probability mass function for a binomial distribution is given by: P(X = k) = nCk pk(1-p)n-k
Substituting the values: P(2 girls) = 3C2 (1⁄2)2(1⁄2)3-2 = 3 x 1⁄4 x 1⁄2 = 3⁄8
Thus, the probability of having exactly two girls and one boy is 3⁄8.
Question 8:
Person 1 and Person 2 invest in three mutual funds A, B, and C. The amounts they invest in each of these mutual funds are given in the table.
| Mutual fund | A | B | C |
|---|---|---|---|
| Person 1 | Rs 10,000 | Rs 20,000 | Rs 20,000 |
| Person 2 | Rs 20,000 | Rs 15,000 | Rs 15,000 |
At the end of one year, the total amount that Person 1 gets is Rs 500 more than Person 2. The annual rate of return for the mutual funds B and C is 15%. What is the annual rate of return for the mutual fund A?
View Solution
Solution: Let the annual rate of return for mutual fund A be r.
- For Person 1, the total amount after one year will be:
Total for Person 1 = 10000 × (1 + r⁄100) + 20000 × (1 + 15⁄100) + 20000 × (1 + 15⁄100)
= 10000 × (1 + r⁄100) + 20000 × 1.15 + 20000 × 1.15
- For Person 2, the total amount after one year will be:
Total for Person 2 = 20000 × (1 + r⁄100) + 15000 × (1 + 15⁄100) + 15000 × (1 + 15⁄100)
= 20000 × 1.15 + 15000 × 1.15 + 15000 × 1.15
We are given that Person 1 gets Rs 500 more than Person 2.
Total for Person 1 – Total for Person 2 = 500
Substitute the expressions for the totals and simplify to find r.
Hence, the correct answer is (B) 10%
Question 9:
Three different views of a dice are shown in the figure below. The piece of paper that can be folded to make this dice is:

View Solution
Solution: To solve this question, we need to determine which arrangement of the numbers on the die satisfies the given views. In a standard die, opposite faces sum to 7, so: 5 and 2 are opposite faces. - 4 and 3 are opposite faces. - 6 and 1 are opposite faces.
By checking the options, we find that option (A) satisfies the conditions: 
Thus, the correct answer is (A).
Question 10:
Visualize two identical right circular cones such that one is inverted over the other and they share a common circular base. If a cutting plane passes through the vertices of the assembled cones, what shape does the outer boundary of the resulting cross-section make?
View Solution
Solution: In this question, we have two identical right circular cones. One cone is inverted over the other, sharing a common circular base. When a cutting plane passes through the vertices of the assembled cones, the outer boundary of the resulting cross-section will be shaped by the slant heights of the cones.
Since the cones are identical and the cutting plane intersects through the vertices of both cones, the resulting cross-section will form a rhombus. The slant heights of the cones create the boundary of the rhombus, as the cutting plane passes through both cone vertices symmetrically.
Thus, the shape of the outer boundary of the cross-section is a rhombus.
Question 11:
• (i) The mean and variance of a Poisson random variable are equal.
• (ii) For a standard normal random variable, the mean is zero and the variance is one.
Which ONE of the following options is correct?
View Solution
Solution: Statement (i) is true for a Poisson random variable, as for a Poisson distribution with parameter λ, both the mean and variance are equal to λ.
- Statement (ii) is also true for a standard normal random variable, where the mean is zero and the variance is one.
Therefore, the correct answer is (A) Both (i) and (ii) are true.
Question 12:
Three fair coins are tossed independently. T is the event that two or more tosses result in heads. S is the event that two or more tosses result in tails. What is the probability of the event T ∩ S?
View Solution
Solution: The possible outcomes of tossing three fair coins are:
{HHH, HHT, HTH, HTT,THH,THT,TTH,TTT}
- T (two or more heads) occurs for: {HHH, HHT, HTH,THH}. - S (two or more tails) occurs for: {HTT,THT,TTH,TTT}.
The intersection T∩S represents the event where there are exactly two heads and two tails. From the list of outcomes, the only outcome satisfying both events is {HTT,THT,TTH}, which occurs with probability 3⁄8.
Thus, the probability of the event T ∩ S is:
P(T∩S) = 3⁄8 = 0.375 -> 0
Question 13:
Consider the matrix . Which ONE of the following statements is TRUE?
. Which ONE of the following statements is TRUE?
View Solution
Solution: The eigenvalues of a matrix M are the solutions to the characteristic equation:
det(M – λI) = 0
For the matrix M = 2 3⁄-1 -1, the characteristic equation is:
det(2 - λ 3⁄-1 -1-λ) = 0
(2 – λ)(−1 – λ) – (−3) = 0
λ2 − λ + 2 + 3 = 0
λ2 + λ + 5 = 0
The discriminant of this quadratic equation is:
Δ = 12 − 4 × 1 × (−5) = 1 + 20 = 21
Since the discriminant is positive, the eigenvalues are real and distinct. Thus, the eigenvalues of M are real and non-negative.
Thus, the correct answer is (D) One eigenvalue of M is non-negative and real, and another eigenvalue of M is negative and real.
Question 14:
Consider performing depth-first search (DFS) on an undirected and unweighted graph G starting at vertex s. For any vertex u in G, d[u] is the length of the shortest path from s to u. Let (u, v) be an edge in G such that d[u] < d[v]. If the edge (u, v) is explored first in the direction from u to v during the above DFS, then (u, v) becomes a - edge.
View Solution
Solution: In depth-first search (DFS), edges are classified into the following types: - Tree edges: Edges that are part of the DFS tree. - Back edges: Edges that connect a vertex to one of its ancestors in the DFS tree. - Cross edges: Edges that connect vertices in different DFS trees. - Forward edges: Edges that connect a vertex to a descendant in the DFS tree.
Since (u, v) is explored first in the direction from u to v and d[u] < d[v], this indicates that (u, v) is a tree edge, as v is discovered from u.
Thus, the correct answer is (A) tree.
Question 15:
For any twice differentiable function f : R → R, if at some x* ∈ R, f'(x*) = 0 and f''(x*) > 0, then the function f necessarily has a _______ at x*.
View Solution
Solution: For a function f, if f'(x*) = 0 and f''(x*) > 0, then x* is a point of local minimum. This is because: - The condition f'(x*) = 0 means that x* is a critical point. - The second derivative test states that if f"(x*) > 0, then the function has a local minimum at x*.
Therefore, the correct answer is local minimum.
Question 16:
Match the items in Column 1 with the items in Column 2 in the following table:
| Column 1 | Column 2 |
|---|---|
| (p) First In First Out | (i) Stacks |
| (q) Lookup Operation | (ii) Queues |
| (r) Last In First Out | (iii) Hash Tables |
View Solution
Solution: - (p) "First In First Out" refers to queues, as they follow the FIFO order. - (q) "Lookup Operation" refers to hash tables, where the primary operation is to lookup values efficiently. - (r) "Last In First Out" refers to stacks, as they follow the LIFO order.
Thus, the correct match is (p) → (ii), (q) → (iii), (r) → (i).
Question 17:
Consider the dataset with six datapoints: {(x1, y1), (x2, y2), ..., (x6, y6)}, where x1 = [0], x2 = [1], x3 = [−1], x4 = [2], x5 = [−2], and the labels are given by y1 = y2 = 5, y3 = y4 = 5, and y5 = y6 = −1. A hard margin linear support vector machine is trained on the above dataset. Which ONE of the following sets is a possible set of support vectors?
View Solution
Solution: For a hard margin linear support vector machine (SVM), support vectors are the data points that lie on or near the decision boundary. In this case, the points with labels y = 5 lie on one side of the boundary and the points with labels y = -1 lie on the other side. The support vectors are the points closest to the decision boundary.
Given the arrangement of data points, the set {x1, x2, x3, x4} forms a valid set of support vectors, as these points are the closest to the margin boundary.
Thus, the correct answer is {x1, x2, x3, x4} .
Question 18:
Match the items in Column 1 with the items in Column 2 in the following table:
| Column 1 | Column 2 |
|---|---|
| (p) Principal Component Analysis | (i) Discriminative Model |
| (q) Naive Bayes Classification | (ii) Dimensionality Reduction |
| (r) Logistic Regression | (iii) Generative Model |
View Solution
Solution: Principal Component Analysis (PCA) is a method for dimensionality reduction, so p corresponds to (ii). - Naive Bayes Classification is a generative model, as it models the joint probability distribution of the features and the class, so q corresponds to (iii). - Logistic Regression is a discriminative model, as it directly models the probability of the class given the features, so r corresponds to (i).
Thus, the correct match is (p) → (i), (q) → (ii), (r) → (iii).
Question 19:
Euclidean distance based k-means clustering algorithm was run on a dataset of 100 points with k = 3. If the points [1, 1] and [−1, -1] are both part of cluster 3, then which ONE of the following points is necessarily also part of cluster 3?
View Solution
Solution: Given that the points [1, 1] and [-1, -1] are both part of cluster 3, the centroid of cluster 3 would likely be near the origin [0, 0], based on the geometry of the points.
Among the provided options, 0⁄1 is the point that lies closest to the origin. Therefore, this point is most likely to be part of cluster 3.
Thus, the correct answer is 0⁄1.
Question 20:
Given a dataset with K binary-valued attributes (where K > 2) for a two-class classification task, the number of parameters to be estimated for learning a naive Bayes classifier is:
View Solution
Solution: In a naive Bayes classifier, for each class, we need to estimate the probabilities for each attribute being 0 or 1. For K binary-valued attributes, the number of parameters to estimate is 2K (for the two possible values of each attribute). Additionally, we need to estimate the class probabilities, which contributes 1 parameter for each class.
Thus, the total number of parameters to estimate is:
2K + 1
Therefore, the correct answer is 2K + 1.
Question 21:
Consider performing uniform hashing on an open address hash table with load factor α < 1, where n elements are stored in the table with m slots. The expected number of probes in an unsuccessful search is at most 1⁄1-α. Inserting an element in this hash table requires at most __ probes, on average.
View Solution
Solution: The number of probes required for an unsuccessful search in a hash table with open addressing can be derived from the expected value of the number of probes in a uniform hashing scheme.
For an unsuccessful search, the expected number of probes is given by the formula:
1⁄1-α
where α= n⁄m is the load factor, n is the number of elements in the table, and m is the number of slots.
For inserting an element into the hash table, the expected number of probes will be the same as the expected number of probes for an unsuccessful search because insertion is similar to searching, except that once an empty slot is found, the element is inserted.
Thus, the correct answer is 1⁄1-α.
Question 22:
For any binary classification dataset, let SB ∈ Rdxd and SW ∈ Rdxd be the between-class and within-class scatter (covariance) matrices, respectively. The Fisher linear discriminant is defined by J(u) = uTSBu⁄uTSWu, that maximizes J(u). If λ = J(u), SW is non-singular and SB ≠ 0, then u*, λ must satisfy which ONE of the following equations?
View Solution
Solution: The Fisher's Linear Discriminant maximization problem can be solved using optimization techniques. By differentiating J(u) = uTSBu⁄uTSWu and setting the derivative equal to zero, we obtain the following equation:
SWSBu* = λu*
where λ is the maximized value of the objective function, and u* is the optimal projection vector.
Thus, the correct answer is SWSBu* = λu*.
Question 23:
Let h1 and h2 be two admissible heuristics used in A* search. Which ONE of the following expressions is always an admissible heuristic?
View Solution
Solution: In A* search, a heuristic is admissible if it never overestimates the true cost to reach the goal. If h1 and h2 are both admissible heuristics, then:
- h1 + h2 is admissible because it sums two admissible heuristics, and the sum is still a lower bound of the actual cost. - h1 × h2 is not necessarily admissible because it could result in overestimation. - h1⁄h2 (with h2 ≠ 0) could also overestimate the true cost depending on the values of h1 and h2. - |h1 - h2| is always admissible because the difference between two admissible heuristics will still be a lower bound.
Thus, the correct answer is |h1 – h2|.
Question 24:
Consider five random variables U, V, W, X, Y whose joint distribution satisfies:
P(U, V, W, X, Y) = P(U)P(V)P(W|U,V)P(X|W)P(Y|W)
Which ONE of the following statements is FALSE?
View Solution
Solution: From the joint distribution, we can analyze the conditional independence: - Y is conditionally independent of V given W, because Y depends only on W and not on V. - X is conditionally independent of U given W, because X depends only on W and not on U. - U and V are not necessarily conditionally independent given W, as they may have a dependency through W. - Y and X are conditionally independent given W, as they are conditionally independent when W is known.
Thus, the correct answer is (C) U and V are conditionally independent given W.
Question 25:
Consider the following statement: In adversarial search, α-β pruning can be applied to game trees of any depth where α is the (m) value choice we have formed so far at any choice point along the path for the MAX player and β is the (n) value choice we have formed so far at any choice point along the path for the MIN player. Which ONE of the following choices of (m) and (n) makes the above statement valid?
View Solution
Solution: In alpha-beta pruning, the idea is to prune branches of the search tree where further exploration will not change the outcome of the game.
For the MAX player, we are interested in maximizing the value, so α is the highest value that the MAX player can guarantee up to that point. - For the MIN player, we are interested in minimizing the value, so β is the lowest value that the MIN player can guarantee up to that point.
Therefore, the correct setting is: - (m) = highest for the MAX player (because we want to maximize the value). - (n) = lowest for the MIN player (because we want to minimize the value).
Thus, the correct answer is (C) (m) = highest, (n) = lowest
Question 26:
Consider a database that includes the following relations: Defender(name, rating, side, goals), Forward(name, rating, assists, goals), Team(name, club, price). Which ONE of the following relational algebra expressions checks that every name occurring in Team appears in either Defender or Forward, where Ø denotes the empty set?
View Solution
Solution: We need to check if every name in the Team relation appears in either the Defender or Forward relations. The correct relational algebra expression would:
- First, project the names from both the Defender and Forward relations using πname(Defender) and πname(Forward). - Then, find the names that are in Team but not in either Defender or Forward. This can be done by subtracting the union of πname(Defender) and πname(Forward) from πname(Team). - Finally, check if the result is the empty set, which means that every name in Team must appear in either Defender or Forward. Thus, the correct expression is:
πname(Team) \ (πname(Defender) ∪ πname(Forward)) = Ø
Question 27:
Let the minimum, maximum, mean, and standard deviation values for the attribute income of data scientists be Rs 246000, Rs 170000, Rs 96000, and Rs 21000, respectively. The Z-score normalized income value of Rs 106000 is closest to which ONE of the following options?
View Solution
Solution: The formula for calculating the Z-score is:
Z = X - μ⁄σ
where: - X is the raw score (Rs 106000), - μ is the mean (Rs 96000), - σ is the standard deviation (Rs 21000).
Substituting the values:
Z = 106000 - 96000⁄21000 = 10000⁄21000 ≈ 0.476
Thus, the Z-score normalized income value of Rs 106000 is closest to 0.476.
Question 28:
Consider the following tree traversals on a full binary tree: • (i) Preorder • (ii) Inorder • (iii) Postorder Which of the following traversal options is/are sufficient to uniquely reconstruct the full binary tree?
View Solution
Solution: To uniquely reconstruct a full binary tree, we need sufficient information about the structure of the tree. For a full binary tree:
- Preorder and Inorder traversals together provide sufficient information to uniquely reconstruct the tree. In Preorder, we visit the root first, and in Inorder, we visit the left subtree, then the root, and then the right subtree. - Inorder and Postorder traversals alone are not sufficient because both traversals can have similar structures for different trees. - Preorder and Postorder together can also be used to reconstruct the tree uniquely.
Thus, the correct answer is (i) and (ii).
Question 29:
Let x and y be two propositions. Which of the following statements is a tautology/are tautologies?
View Solution
Solution: - In option (A), the expression (¬x∧y) ⇒ (y ⇒ x) is not a tautology as it does not always hold true for every possible value of x and y. - In option (B), the expression (x ∧ ¬y) ⇒ (¬x ⇒ y) is not a tautology. - In option (C), the expression (¬x ∨ y) ⇒ (¬x ⇒ y) is a tautology because it holds true for all possible truth values of x and y. - In option (D), (x ∧ ¬y) ⇒ (y ⇒ x) is not a tautology either.
Thus, the correct answer is (C) (¬x ∨ y) ⇒ (¬x ⇒ y).
Question 30:
Consider sorting the following array of integers in ascending order using an in-place Quicksort algorithm that uses the last element as the pivot.
{60, 70, 80, 90, 100} The minimum number of swaps performed during this Quicksort is:
View Solution
Solution: In the in-place Quicksort algorithm using the last element as the pivot, the array is divided into smaller partitions recursively, and elements are swapped into their correct position.
Here, the array is already sorted in ascending order. During the first partitioning step, the pivot (100) will already be in its correct position. No swaps are needed for other elements, as they are already correctly placed.
Thus, the minimum number of swaps performed during this Quicksort is 0.
Question 31:
Consider the following two tables named Raider and Team in a relational database maintained by a Kabaddi league. The attribute ID in table Team references the primary key of the Raider table, ID.
Raider table:
| ID | Name | Raids | RaidPoints |
|---|---|---|---|
| 1 | Arjun | 190 | 250 |
| 2 | Ankush | 190 | 219 |
| 3 | Sunil | 150 | 200 |
| 4 | Reza | 150 | 190 |
| 5 | Pratham | 175 | 220 |
| 6 | Gopal | 193 | 215 |
Team table:
| City | ID | BidPoints |
|---|---|---|
| Jaipur | 2 | 200 |
| Patna | 3 | 195 |
| Hyderabad | 5 | 175 |
| Jaipur | 2 | 250 |
| Patna | 4 | 200 |
| Jaipur | 6 | 200 |
The SQL query described below is executed on this database:
SELECT *
FROM Raider, Team
WHERE Raider.ID = Team.ID AND City = "Jaipur" AND RaidPoints > 200;
The number of rows returned by this query is:
View Solution
Solution: Let's break down the SQL query:
- The query selects data from the Raider and Team tables, joining them on the condition Raider.ID = Team.ID. - It filters the data where the City is "Jaipur" and the RaidPoints are greater than 200.
Looking at the data:
- The City "Jaipur" appears in the Team table with ID 2 and ID 6. - For ID 2, the corresponding Raider table has RaidPoints 250, which satisfies the condition RaidPoints > 200. - For ID 6, the corresponding Raider table has RaidPoints 215, which also satisfies the condition RaidPoints > 200. - For ID 2, the corresponding Raider table has RaidPoints 250 again, which also satisfies the condition.
Thus, three rows will be returned by this query.
Question 32:
The fundamental operations in a double-ended queue D are:
• insertFirst(e) = Insert a new element e at the beginning of D.
• insertLast(e) = Insert a new element e at the end of D.
• removeFirst() = Remove and return the first element of D.
• removeLast() = Remove and return the last element of D.
In an empty double-ended queue, the following operations are performed:
• insertFirst(10)
• insertLast(32)
• a ← removeFirst()
• insertLast(28)
• insertLast(17)
• a ← removeFirst()
• a ← removeLast()
The value of a is _____
View Solution
Solution: Let's break down the operations step-by-step:
1. insertFirst(10): The queue becomes [10].
2. insertLast(32): The queue becomes [10,32].
3. a ← removeFirst(): This removes 10, so a = 10, and the queue becomes [32].
4. insertLast(28): The queue becomes [32, 28].
5. insertLast(17): The queue becomes [32, 28, 17].
6. a ← removeFirst(): This removes 32, so a = 32, and the queue becomes [28,17].
7. a ← removeLast(): This removes 17, so a = 17, and the queue becomes [28].
Thus, the value of a is 17.
Question 33:
Let f: R → R be the function f(x) = 1⁄1+e-x. The value of the derivative of f at x where f(x) = 0.4 is _____ (rounded off to two decimal places).
View Solution
Solution: The given function is f(x) = 1⁄1+e-x, which is the logistic function. The derivative of f(x) is given by:
f'(x) = f(x)(1 − f(x))
We are asked to find f'(x) when f(x) = 0.4.
Substituting f(x) = 0.4 into the derivative formula:
f'(x) = 0.4 × (1 – 0.4) = 0.4 x 0.6 = 0.24
Thus, the value of the derivative at x where f(x) = 0.4 is 0.24.
Question 34:
The sample average of 50 data points is 40. The updated sample average after including a new data point taking the value of 142 is ____
View Solution
Solution: The sample average x is given by:
x = Σni=1 xi⁄n
For n = 50, the sample average is 40, so the sum of the data points is:
Σ50i=1 xi = 40 × 50 = 2000
After including the new data point, the new sum becomes:
Σ51i=1 xi = 2000 + 142 = 2142
The updated sample average is:
xnew = 2142⁄51 = 42
Thus, the updated sample average is 42.
Question 35:
Consider the 3 × 3 matrix  . The determinant of M2 + 12M is ___.
. The determinant of M2 + 12M is ___.
View Solution
Solution: We are asked to find the determinant of M2 + 12M. First, calculate M2:
M2 = 1 2 3⁄3 1 1 x 1 2 3⁄3 1 1
4 3 6⁄4 3 6
Multiplying these matrices:
M2 = 1(1)+2(3)+3(4) 1(2)+2(1)+3(3) 1(3)+2(1)+3(6)⁄3(1)+1(3)+1(4) 3(2)+1(1)+1(3) 3(3)+1(1)+1(6)
4(1)+3(3)+6(4) 4(2)+3(1)+6(3) 4(3)+3(1)+6(6)
This results in:
M2 = 1+6+12 2+2+9 3+2+18⁄3+3+4 6+1+3 9+1+6 = 19 13 23⁄10 10 16
4+9+24 8+3+18 12+3+36⁄37 29 51
Now add 12M:
12M = 12 × 1 2 3⁄3 1 1 = 12 24 36⁄36 12 12
4 3 6⁄48 36 72
Now calculate M2+12M:
M2 + 12M = 19 13 23⁄10 10 16 + 12 24 36⁄36 12 12
37 29 51⁄48 36 72
M2 + 12M = 31 37 59⁄46 22 28
85 65 123
Finally, compute the determinant of this matrix: det(M2 + 12M) = 31 × det22 28⁄65 123 − 37 × det46 28⁄85 123+ 59 × det 46 22⁄85 65
Computing the determinants, we find that the determinant is 0.
Thus, the correct answer is 0.
Question 36:
A fair six-sided die (with faces numbered 1, 2, 3, 4, 5, 6) is repeatedly thrown independently. What is the expected number of times the die is thrown until two consecutive throws of even numbers are seen?
View Solution
Solution: Let us define the states as follows: - State 0: No even number has been thrown yet. - State 1: One even number has been thrown, and we are waiting for the second consecutive even number. - State 2: Two consecutive even numbers have been thrown, and the process ends. From State 0, the probability of throwing an even number (2, 4, or 6) is 3⁄6 = 1⁄2, and the probability of throwing an odd number (1, 3, or 5) is also 1⁄2.
From State 1, if an even number is thrown, we reach State 2, completing the sequence of two consecutive even throws. If an odd number is thrown, we revert to State 0.
To calculate the expected number of throws: - The expected number of throws to go from State 0 to State 1 is 2. - From State 1 to State 2, the expected number of throws is 2 as well (since you either end with two even numbers or revert to State 0).
Hence, the total expected number of throws is 2 + 2 = 6.
Thus, the correct answer is 6.
Question 37:
Let f : R → R be a function. Note: R denotes the set of real numbers. f(x) = -x, if x < -2⁄ax2 + bx + c, if x ∈ [-2, 2] x, if x > 2
Which ONE of the following choices gives the values of a, b, and c that make the function f continuous and differentiable?
View Solution
Solution: We are asked to make the function f(x) continuous and differentiable. We will do this by ensuring that: 1. f(x) is continuous at the points where the piecewise definitions change, i.e., at x = -2 and x = 2. 2. f(x) is differentiable at the points where the piecewise definitions change.
Step 1: Continuity at x = -2 and x = 2
For continuity at x = -2, we must have the value of f(x) from both sides equal: limx→-2- f(x) = limx→-2+ f(x)
From the left-hand side, f(x) = -x, so:
limx→-2- f(x) = -(-2) = 2
From the right-hand side, f(x) = ax2 + bx + c, so:
f(-2) = a(-2)2 + b(−2) + c = 4a – 2b + c
For continuity, we require:
4a - 2b + c = 2 (Equation 1)
For continuity at x = 2, we must have:
limx→2- f(x) = limx→2+ f(x)
From the left-hand side, f(x) = ax2 + bx + c, so:
f(2) = a(2)2 + b(2) + c = 4a + 2b + c
From the right-hand side, f(x) = x, so:
f(2) = 2
For continuity, we require:
4a + 2b + c = 2 (Equation 2)
Step 2: Differentiability at x = -2 and x=2
For differentiability at x = -2, we require:
limx→-2- f'(x) = limx→-2+ f'(x)
The derivative of f(x) = -x is f'(x) = -1, and the derivative of f(x) = ax2 + bx + c is:
f'(x) = 2ax + b
At x = -2, we require:
f'(-2) = -1 and 2a(-2) + b = -1
Simplifying:
-4a + b = -1 (Equation 3)
For differentiability at x = 2, we require:
limx→2- f'(x) = limx→2+ f'(x)
The derivative of f(x) = ax2 + bx + c at x = 2 is:
f'(2) = 2a(2) + b = 4a + b
The derivative of f(x) = x is f'(x) = 1, so we require:
4a + b = 1 (Equation 4)
Step 3: Solve the system of equations
From Equations 3 and 4:
-4a + b = -1 and 4a + b = 1
Adding these two equations eliminates b:
2b = 0 -> b = 0
Substituting b = 0 into Equation 4:
4a = 1 -> a = 1⁄4
Substituting a = 1⁄4 and b = 0 into Equation 1:
4a - 2b + c = 2 4(1⁄4) - 2(0) + c = 2
1 + c = 2 -> c = 1
Thus, the values of a, b, and c are:
a = 1⁄4, b = 0, c = 1
Thus, the correct answer is a = 1⁄4, b = 0, c = 1.
Question 38:
Consider the following Python code:
def count(child_dict, i):
if i not in child_dict.keys():
return 1
ans = 1
for j in child_dict[i]:
ans += count(child_dict, j)
return ans
child_dict = dict()
child_dict[0] = [1,2]
child_dict[1] = [3,4,5]
child_dict[2] = [6,7,8]
print(count(child_dict,0))
Which ONE of the following is the output of this code?
View Solution
Solution: Let's analyze the code again carefully:
We have a dictionary child_dict that represents a tree structure, where each key in the dictionary corresponds to a node, and the value is a list of child nodes. The function count(child_dict, i) counts the number of nodes in the subtree rooted at node i, including the node i itself.
Step-by-step Execution:
1. The function is initially called with i = 0: - child_dict[0] = [1,2], so the function calls count(child_dict, 1) and count(child_dict, 2).
2. For i = 1: - child_dict[1] = [3,4,5], so the function calls count(child_dict, 3), count(child_dict, 4),and count(child_dict, 5).
3. For i = 2: - child_dict[2] = [6,7,8], so the function calls count(child_dict, 6), count(child_dict, 7),and count(child_dict, 8).
4. For all the nodes i = 3, 4, 5, 6, 7, 8, there are no children, so the function returns 1 for each of these calls (base case).
Calculating the Total:
- For i = 0:
ans = 1 + count(child_dict, 1) + count(child_dict, 2)
- For i = 1:
ans = 1+count(child_dict, 3)+count(child_dict, 4)+count(child_dict, 5) = 1 + 1 + 1 + 1 = 4
- For i = 2:
ans = 1+count(child_dict, 6)+count(child_dict, 7)+count(child_dict, 8) = 1+1+1+1=4
- For i = 0, the total count is:
ans = 1 + 4 + 4 = 9
Thus, the correct output is 9.
Question 39:
Consider the function computeS(X) whose pseudocode is given below:
computeS(X)
S[1] = 1
for i = 2 to length(X)
S[i] = -1
if X[i-1] <= X[i]
S[i] = S[i-1] + S[i-1]
end if
end for
return S
Which ONE of the following values is returned by the function computeS(X) for X = [6, 3, 5, 4, 10]?
View Solution
Solution: We are given the function computeS(X) that initializes an array S based on the array X.
Let's go through the pseudocode step by step with X = [6, 3, 5, 4, 10]:
1. Initialize S[1] = 1. 2. For each i from 2 to 5, execute the following logic: - i = 2: X[1] = 6, X[2] = 3, since X[1] > X[2], set S[2] = −1. - i = 3: X[2] = 3, X[3] = 5, since X[2] < X[3], set S[3] = S[2] + S[1] = −1 + 1 = 0. - i = 4: X[3] = 5, X[4] = 4, since X[3] > X[4], set S[4] = -1. - i = 5: X[4] = 4, X[5] = 10, since X
Solution: We are given the function computeS(X) that initializes an array S based on the array X.
Let's go through the pseudocode step by step with X = [6, 3, 5, 4, 10]:
1. Initialize S[1] = 1. 2. For each i from 2 to 5, execute the following logic: - i = 2: X[1] = 6, X[2] = 3, since X[1] > X[2], set S[2] = −1. - i = 3: X[2] = 3, X[3] = 5, since X[2] < X[3], set S[3] = S[2] + S[1] = −1 + 1 = 0. - i = 4: X[3] = 5, X[4] = 4, since X[3] > X[4], set S[4] = -1. - i = 5: X[4] = 4, X[5] = 10, since X[4] < X[5], set S[5] = S[4] + S[3] = −1 + 0 = −1.
After the function completes execution, the array S becomes:
S = [1, -1, 0, -1, -1]
Thus, the correct answer is [1, -1, 0, -1, -1].
Question 40:
Let F(n) denote the maximum number of comparisons made while searching for an entry in a sorted array of size n using binary search. Which ONE of the following options is TRUE?
View Solution
Solution: The maximum number of comparisons in binary search occurs when we divide the problem size by 2 at each step, and we add one comparison for each division. Therefore, the recurrence relation is:
F(n) = F(n⁄2) + 1.
Thus, the correct option is (A).
Question 41:
Consider the following Python function:
def fun(D, s1, s2):
if s1 < s2:
D[s1], D[s2] = D[s2], D[s1]
fun(D, s1+1, s2-1)
What does this Python function fun() do? Select the ONE appropriate option below.
View Solution
Solution: The function recursively swaps the elements at indices s1 and s2, and then continues with the next pair of elements by incrementing s1 and decrementing s2. This continues until s1 is no longer less than s2. Essentially, this results in reversing the sublist between indices s1 and s2.
Thus, the correct option is (C).
Question 42:
Consider the table below, where the (i, j)th element of the table is the distance between points xi and xj. Single linkage clustering is performed on data points x1, x2, x3, x4, x5:
| x1 | x2 | x3 | x4 | x5 | |
|---|---|---|---|---|---|
| x1 | 0 | 1 | 4 | 3 | 6 |
| x2 | 1 | 0 | 3 | 5 | 3 |
| x3 | 4 | 3 | 0 | 2 | 5 |
| x4 | 3 | 5 | 2 | 0 | 1 |
| x5 | 6 | 3 | 5 | 1 | 0 |
Which ONE of the following is the correct representation of the clusters produced?
Cluster 2: x3
Cluster 3: x4, x5
View Solution
Solution: In single linkage clustering, we start by finding the smallest distance between any two points and merge the two clusters. We then repeat the process by finding the smallest distance between any two clusters. From the table: - The minimum distance between x1 and x2 is 1. - The minimum distance between x3 and x4 is 2. - The minimum distance between x4 and x5 is 1. Thus, the clusters will eventually merge into the structure:
Cluster 1: x1, x2, Cluster 2: x3, Cluster 3: x4, x5.
So, the correct option is (A).
Question 43:
Consider the two neural networks (NNs) shown in Figures 1 and 2, with ReLU activation, where ReLU(z) = max{0,z}, ∀z∈ R. The connections and their corresponding weights are shown in the figures. The biases at every neuron are set to 0. For what values of p, q, and r in Figure 2 are the two neural networks equivalent, given that x1, x2, and x3 are positive?4


View Solution
Solution: Given that the activation function is ReLU, we know that the output of a neuron is the maximum of 0 and the weighted sum of its inputs. To determine when the two neural networks are equivalent, we need to consider how the input values x1, x2, and x3 relate to the weights p, q, and r in both networks.
Since the exact figures and the structure of the neural networks are not provided in the question, we can only analyze the potential relationships between the weights. The networks will be equivalent when the relationships between the weighted sums in both networks produce identical outputs for all positive inputs x1, x2, and x3. The key to determining the equivalence is ensuring that the output of each network, as a function of the weights and inputs, is the same for all possible values of x1, x2, and x3.
Answer: (B) p = 24, q = 24, r = 36
Question 44:
Consider a state space where the start state is number 1. The successor function for the state numbered n returns two states numbered n + 1 and n + 2. Assume that the states in the unexpanded state list are expanded in the ascending order of numbers and the previously expanded states are not added to the unexpanded state list. Which ONE of the following statements about breadth-first search (BFS) and depth-first search (DFS) is true, when reaching the goal state number 6?
View Solution
Solution: For both BFS and DFS, the expansion of states is based on the rule that each state n leads to two states: n + 1 and n + 2. Starting from state 1: - BFS would expand states level by level: - First, it expands 1 → 2 and 3. - Next, it expands 2 → 3, and 3 → 4, etc. - DFS would expand deeper into the tree: - First, it expands 1 → 2, then 2 → 3, then 3 → 4, and so on. In both cases, the same states are expanded to reach state 6. Thus, both BFS and DFS expand the same number of states. Thus, the correct answer is (C).
Question 45:
Consider the following sorting algorithms: • (i) Bubble sort • (ii) Insertion sort • (iii) Selection sort Which ONE among the following choices of sorting algorithms sorts the numbers in the array [4, 3, 2, 1, 5] in increasing order after exactly two passes over the array?
View Solution
Solution: Let's analyze the sorting algorithms: - Bubble sort after two passes: - First pass: [3, 2, 1, 4, 5] → [2, 1, 3, 4, 5] - Second pass: [1, 2, 3, 4, 5] - After two passes, the array is sorted. - Insertion sort after two passes: - First pass: [3, 4, 2, 1, 5] - Second pass: [2, 3, 4, 1, 5] - The array is not yet sorted after two passes. - Selection sort after two passes: - First pass: [1, 3, 2, 4, 5] - Second pass: [1, 2, 3, 4, 5] - After two passes, the array is sorted. Therefore, Selection sort (iii) will sort the array in two passes, but Bubble sort (i) will not sort it in exactly two passes. Thus, the correct answer is (B).
Question 46:
Given the relational schema R = (U, V, W, X, Y, Z) and the set of functional dependencies:
{U → V, U → W, W → Y, W → Z, X → Y, X → Z} Which of the following functional dependencies can be derived from the above set?
View Solution
Solution: Step 1: Identify the Functional Dependencies in the Given Set
The given set of functional dependencies is:
{U → V, U → W, W → Y, W → Z, X → Y, X → Z}
Step 2: Derive New Functional Dependencies
Let's check the possible derivations:
- VW → YZ can be derived as follows: - From W → Y and W → Z, we can conclude that VW → YZ.
- WX → YZ can also be derived because: - From X → Y and X → Z, we can conclude that WX → YZ.
- VW → Y can be derived because: - From W → Y, we know that knowing W implies Y.
Final Answer:
VW → YZ, WX → YZ, VW → Y
Question 47:
Select all choices that are subspaces of R3.
Note: R denotes the set of real numbers.
View Solution
Solution: Step 1: Check for Subspace Criteria
To determine if the given set is a subspace, we must check if the set satisfies the following conditions: 1. Contains the zero vector. 2. Closed under addition. 3. Closed under scalar multiplication.
Step 2: Evaluate the Options
- Option (A): The given set consists of all linear combinations of two vectors 1⁄1⁄0 and 1⁄0⁄1, which is a subspace of R3 because it satisfies all subspace properties.
- Option (B): The set involves quadratic terms α2 and β2, which disqualifies it as a subspace because the elements are not closed under scalar multiplication. Thus, this is not a subspace.
- Option (C): The set consists of the solutions to a system of linear equations, and thus forms a subspace because it satisfies all subspace properties.
- Option (D): The equation 5x1 + 2x3 + 4 = 0 does not pass through the origin, hence it is not a subspace.
Final Answer:
A, C
Question 48:
Which of the following statements is/are TRUE?
Note: R denotes the set of real numbers.
View Solution
Solution: Step 1: Analyze Each Option
- Option (A): If M ∈ R3x3, for Mx = p to have a unique solution, M must be invertible. However, if Mx = q has infinite solutions, M must be singular, which contradicts the assumption of invertibility. Hence, this option is false.
- Option (B): If M ∈ R3x3 and Mx = p has no solution, it means that M is singular, and the rank of M is less than 3. If Mx = q has infinite solutions, this is possible if M is singular. Hence, this option is true.
- Option (C): If M ∈ R3x2, then Mx = p cannot have a unique solution because the system has more variables than equations. Thus, this option is false.
- Option (D): If M ∈ R3x2, Mx = p having a unique solution is not possible, as the system has more variables than equations. However, if Mx = q has no solutions, this is possible for a consistent system that has no solution. Hence, this option is true.
Final Answer:
B, D
Question 49:
Let R be the set of real numbers, U be a subspace of R3, and M ∈ R3x3 be the matrix corresponding to the projection onto the subspace U. Which of the following statements is/are TRUE?
View Solution
Solution: Step 1: Understanding the Projection Matrix M
A projection matrix M onto a subspace U satisfies: 1. M2 = M (idempotent property of projection matrices). 2. The null space N(M) consists of all vectors that are projected to zero.
Step 2: Evaluating the Given Statements
- Option (A): If U is a 1-dimensional subspace of R3, then the rank of M is 1, meaning the null space should be 2-dimensional, not 1-dimensional. Hence, this statement is false.
- Option (B): If U is a 2-dimensional subspace of R3, then the rank of M is 2, meaning the null space has dimension 3 – 2 = 1. This statement is true.
- Option (C): Projection matrices satisfy M2 = M, meaning applying the projection twice gives the same result. Hence, this statement is true.
- Option (D): Since M2 = M, multiplying again by M gives M3 = M2, which holds true for any projection matrix. Hence, this statement is true.
Final Answer:
B, C, D
Question 50:
Consider the function f : R → R defined as:
f(x) = x4 - 3x2 + 1⁄x2 + 3. Which of the following statements is/are TRUE?
View Solution
Solution: To analyze the critical points and their nature, we proceed as follows:
1. Critical Points: We first compute the derivative of f(x) and set it to zero to find the critical points.
f(x) = x4 - 3x2 + 1⁄x2 + 3
Let g(x) = x4 - 3x2 + 1 and h(x) = x2 + 3. Using the quotient rule:
f'(x) = g'(x)h(x) - g(x)h'(x)⁄(h(x))2
After simplifying, we find the critical points x = 0, ±1, ±√3.
2. Second Derivative Test: Evaluate f''(x) at the critical points to determine the nature of each:
At x = 0, f''(0) < 0, so x = 0 is a local maximum.
At x = 3, f''(3) > 0, so x = 3 is a local minimum.
At x = −1, f''(-1) < 0, so x = -1 is a local maximum.
Answer: (A), (B), and (C)
Question 51:
Consider the directed acyclic graph (DAG) below:

Which of the following is/are valid vertex orderings that can be obtained from a topological sort of the DAG?
View Solution
Solution: Step 1: Understanding Topological Sorting
A topological sorting of a DAG is a linear ordering of vertices such that for every directed edge (A → B), vertex A appears before vertex B.
Step 2: Identifying the DAG Structure
From the given DAG: - P and R are sources (have no incoming edges). - Q is dependent on P and R. - S and V depend on Q. - U depends on S, and T depends on V.
Step 3: Evaluating the Given Options
- Option (A): PQRSTUV - This order is incorrect because S appears before V, but both must follow Q correctly. - T must appear after V, but it appears earlier. - Incorrect.
- Option (B): PRQVSUT - This ordering correctly follows the dependency structure. - P, R appear before Q, which appears before V and S, followed by U and T. - Correct.
- Option (C): PQRSVUT - P and Q appear before R, which violates the dependency order. - Incorrect.
- Option (D): PRQSVTU - P and R appear before Q, which is correct. - S and V follow Q, maintaining the correct order. - T appears before U, which does not violate any dependency constraints. - Correct.
Final Answer: B, D
Question 52:
Let H, I, L, and N represent height, number of internal nodes, number of leaf nodes, and the total number of nodes respectively in a rooted binary tree. Which of the following statements is/are always TRUE?
View Solution
Solution: Step 1: Understanding the Binary Tree Structure
For a rooted binary tree: - The height H is the length of the longest path from the root to a leaf. - The number of internal nodes I is the number of non-leaf nodes. - The number of leaf nodes L is the number of nodes that do not have children. - The total number of nodes N is the sum of the internal nodes and leaf nodes.
We also know from binary tree properties: - The number of leaf nodes L in a perfect binary tree of height H is L = 2H. - The total number of nodes N in a binary tree is given by N = I + L, and for a complete binary tree, N = 2H+1 - 1.
Step 2: Evaluating the Given Options
- Option (A): L ≤ I + 1 - This is always true because the number of leaf nodes L is at most one more than the number of internal nodes I in any binary tree. - Correct.
- Option (B): H + 1 ≤ N ≤ 2H+1 - 1 - This is true because: - The minimum number of nodes in a binary tree is H + 1, corresponding to a tree where each internal node has only one child (a skewed tree). - The maximum number of nodes occurs when the tree is complete, and this is given by 2H+1 - 1. - Correct.
- Option (C): H ≤ I ≤ 2H - 1 - This is true because the number of internal nodes I is at least H (in a complete binary tree) and at most 2H - 1 (in a perfect binary tree). - Correct.
- Option (D): H ≤ L ≤ 2H - 1 - This is not always true because the number of leaf nodes L is at least 2H for a perfect binary tree, but not necessarily less than 2H - 1. - Incorrect.
Final Answer:
A, B, C
Question 53:
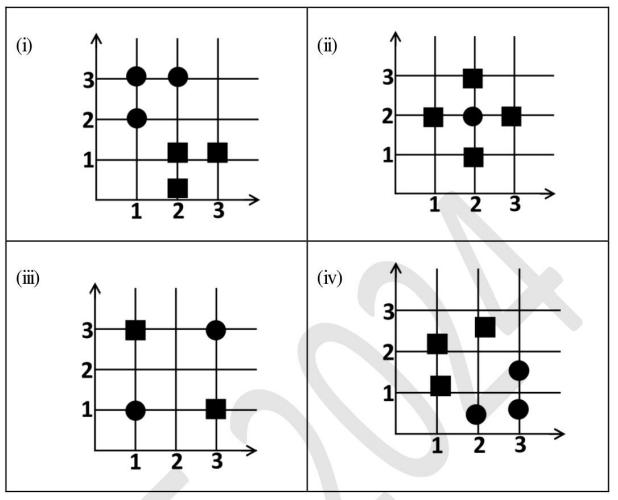
Consider the following figures representing datasets consisting of two-dimensional features with two classes denoted by circles and squares.
Which of the following is/are TRUE?
View Solution
Solution: Step 1: Understanding Linear Separability
A dataset is said to be linearly separable if there exists a straight line (in 2D) or a hyperplane (in higher dimensions) that can separate the two classes without any misclassification.
Step 2: Analyzing the Given Figures
- Figure (i): The circles and squares can be separated by a straight line, as they are clearly divided by the line x1 = 2. - Correct.
- Figure (ii): The circles and squares are not linearly separable. No single straight line can separate them. - Incorrect.
- Figure (iii): The circles and squares are not linearly separable because they overlap, and no straight line can separate them. - Incorrect.
- Figure (iv): The circles and squares can be separated by a straight line, as they are divided along the axis. - Correct.
Final Answer:
A, D
Question 54:
Let game(ball, rugby) be true if the ball is used in rugby and false otherwise. Let shape(ball, round) be true if the ball is round and false otherwise. Consider the following logical sentences: s1 : ∀ball ⇒ game(ball, rugby) ⇒ shape(ball, round) s2 : ∀ball ⇒ ¬shape(ball,round) ⇒ game(ball, rugby) s3 : ∀ball game(ball, rugby) ⇒ ¬shape(ball, round) s4 : ∀ball shape(ball, round) ⇒ ¬game(ball, rugby) Which of the following choices is/are logical representations of the assertion, "All balls are round except balls used in rugby"?
View Solution
Solution: Step 1: Understanding the Assertion ”All balls are round except balls used in rugby"
The assertion means that all balls are round except those used in rugby, i.e., if a ball is used in rugby, it is not round. This statement can be represented logically as: - game(ball, rugby) ⇒ ¬shape(ball, round) (If a ball is used in rugby, it is not round). - ¬game(ball, rugby) ⇒ shape(ball, round) (If a ball is not used in rugby, it must be round).
Step 2: Evaluating the Options
- Option (A): s1 ∧ s3 - s1 is ∀ball ⇒ game(ball, rugby) ⇒ shape(ball, round), which is not the correct representation for "All balls are round except those used in rugby". s3 is ∀ball game(ball, rugby) ⇒ ¬shape(ball, round), which is the correct representation for the "except" part of the assertion. - The combination of s1 and s3 correctly captures the structure of the assertion. - Correct.
- Option (B): s1 ∧ s2 - s2 is ∀ball ⇒ ¬shape(ball, round) ⇒ game(ball, rugby), which is not equivalent to the assertion and does not make logical sense in this context. - Incorrect.
- Option (C): s2 ∧ s3 - s2 is ∀ball ⇒ ¬shape(ball, round) ⇒ game(ball, rugby), which is incorrect. s3 is correct, and it complements the logic by specifying that if a ball is used in rugby, it is not round. - The combination of s2 and s3 accurately captures the assertion's meaning. - Correct.
- Option (D): s3 ∧ s4 - s4 is ∀ball shape(ball, round) ⇒ ¬game(ball, rugby), which is incorrect as it states that a round ball cannot be used in rugby, which contradicts the given context. - Incorrect.
Final Answer:
A, C
Question 55:
An OTT company is maintaining a large disk-based relational database of different movies with the following schema:
• Movie (ID, CustomerRating)
• Genre (ID, Name)
• Movie_Genre (MovieID, GenreID)
The given SQL query is:
SELECT *
FROM Movie, Genre, Movie_Genre
WHERE Movie.CustomerRating > 3.4
AND Genre.Name = "Comedy"
AND Movie_Genre.MovieID = Movie.ID
AND Movie_Genre.GenreID = Genre.ID;
Problem Statement: This SQL query can be sped up using which of the following indexing options?
View Solution
Solution: The query involves the following conditions:
1. Filtering rows based on Movie.CustomerRating > 3.4, which would benefit from a B+ tree index because it supports range queries efficiently.
2. Filtering rows where Genre.Name = "Comedy", which would benefit from a Hash index because hash indexes are efficient for equality searches.
3. Joining the Movie_Genre table with Movie and Genre tables, which would benefit from indexes on the foreign key columns Movie_Genre.MovieID and Movie_Genre.GenreID
The optimal choice for speeding up this query is a Hash index on Genre.Name for equality filtering and a B+ tree index on the remaining attributes for range queries and joins.
Question 56:
Let X be a random variable uniformly distributed in the interval [1, 3] and Y be a random variable uniformly distributed in the interval [2, 4]. If X and Y are independent of each other, the probability P(X > Y) is:
View Solution
Solution: The probability density functions (PDFs) of X and Y are:
fX(x) = 1⁄2 for x ∈ [1,3]
0 otherwise
fY(y) = 1⁄2 for y ∈ [2,4]
0 otherwise
Since X and Y are independent, their joint PDF is:
fx,y(x,y) = fx(x)fy(y) = 1⁄4 for x ∈ [1,3] and y ∈ [2, 4]
0 otherwise.
To compute P(X > Y), we evaluate:
P(X > Y) = ∫∫ fx,y(x, y) dx dy
y=2 x=y
Step 1: Evaluate the limits of integration
- For y ∈ [2,3]: x ∈ [y, 3] - For y ∈ [3, 4]: x ∈ [3, 3] (no contribution since x > y)
Thus, the integral simplifies to:
P(X > Y) = ∫3y=2 ∫3x=y 1⁄4 dx dy
Step 2: Solve the integral
The inner integral over x is: ∫3x=y 1⁄4 dx = 1⁄4 x|3y = 1⁄4(3-y)
The outer integral over y becomes:
∫3y=2 1⁄4(3-y) dy
Simplify:
∫3y=2 1⁄4(3-y) dy= 1⁄4 [3y - y2⁄2]32 = 1⁄4 ( (9 - 9⁄2) - (6 - 4⁄2) ) = 1⁄4( 9⁄2 - 4) = 1⁄4 x 1⁄2 = 5⁄8 Thus:
P(X > Y) = 5⁄8 x 1⁄4 = 5⁄32 ≈ 0.625
Final Answer: 0.625 (rounded off to three decimal places).
Question 57:
Let X be a random variable exponentially distributed with parameter λ > 0. The probability density function (PDF) of X is given by:
fx(x) = λe-λx for x ≥ 0⁄0 otherwise
Given that E(X) = Var(X), where E(X) and Var(X) indicate the expectation and variance of X, respectively, the value of λ is:
View Solution
Solution: The expectation and variance of an exponential random variable with rate parameter λ are:
E(X) = 1⁄λ
Var(X) = 1⁄λ2
Given that E(X) = Var(X), we have:
1⁄λ = 1⁄λ2
Solving for λ:
λ = 1
Final Answer: λ = 1.
Question 58:
Consider two events T and S. Let T denote the complement of the event S. The probability associated with different events are given as follows:
P(T) = 0.6, P(S|T) = 0.3, P(S|T) = 0.6.
We are asked to find P(T|S), the conditional probability of T given S.
View Solution
Solution: Using Bayes' Theorem, we have:
P(T|S) = P(S|T) • P(T)⁄P(S)
Now, we need to calculate P(S). We can use the law of total probability:
P(S) = P(S|T) • P(T) + P(S|T) • P(T)
Substitute the given values:
P(S) = (0.6) • (0.6) + (0.3) • (0.4)
P(S) = 0.36 + 0.12 = 0.48
Now, apply Bayes' Theorem:
P(T|S) = (0.6) • (0.6)⁄0.48= 0.36⁄0.48 = 0.75
Final Answer: P(T|S) = 0.75.
Question 59:
Consider a joint probability density function of two random variables X and Y :
fx,y(x,y) = 2xy, 0 < x < 2, 0
Then, E[Y|X = 1.5] is ____.
View Solution
Solution: Step 1: Compute the Conditional Density Function
The marginal density of X is given by:
fx(x) = ∫x0 2xy dy = 2x y2⁄2 |x0 = x3, 0
The conditional density function of Y given X = x is:
fy|x(y|x) = fx,y(x,y)⁄fx(x) = 2xy⁄x3 = 2y⁄x2, 0
Step 2: Compute E[Y|X = 1.5] The expectation of Y given X = x is:
E[Y|X = x] = ∫x0 y fy|x(y|x) dy = ∫x0 y( 2y⁄x2 ) dy = 2⁄x2 ∫x0 y2 dy = 2⁄x2 [y3⁄3]x0 = 2x3⁄3x2 = 2x⁄3
Substituting x = 1.5:
E[Y|X = 1.5] = 2(1.5)⁄3 = 1
Final Answer: 1
Question 60:
Evaluate the following limit: limx→0 ln((x2 + 1) cos(x))
View Solution
Solution: First, simplify the expression inside the logarithm:
ln((x2 + 1) cos(x)) = ln(x2 + 1) + ln(cos(x))
Now, evaluate the limits of each term separately as x → 0:
limx→0 ln(x2 + 1) = ln(1) = 0
limx→0 ln(cos(x)) = ln(1) = 0
Thus, the overall limit is: limx→0 ln((x2 + 1) cos(x)) = 0 + 0 = 0 Final Answer: 0.
Question 61:
Let u = 1⁄3, and let σ1, σ2, σ3,... be the singular values of the matrix M = uuT (where uT is the transpose of u). The value of σ1σ2...σn is:
View Solution
Solution: Given the matrix M = uuT, where u = 1⁄3, we can calculate the singular values of the matrix. The singular values of a matrix M are the square roots of the eigenvalues of the matrix MTM or MMT.
1. Matrix Calculation:
First, calculate M = uuT:
M = 1⁄3(1 3) = 1 3⁄3 9
2. Singular Values:
The matrix M is a 2 × 2 matrix. To find its singular values, we calculate the eigenvalues of MMT.
MMT = 1 3⁄3 9 * ( 1 3⁄3 9) = 10 30⁄30 90
To find the eigenvalues, solve the characteristic equation det (MMT – λI) = 0: det(10 - λ 30⁄30 90-λ) = (10 - λ)(90 - λ) – 302 = 0
λ2 – 100λ = 0
λ(λ – 100) = 0
Thus, the eigenvalues are λ1 = 0 and λ2 = 100. The singular values of M are the square roots of the eigenvalues:
σ1 = √100 = 10, σ2= 0
3. Final Answer:
Since the product of singular values is σ1·σ2, we have:
σ1σ2 = 10 x 0 = 0.
Final Answer: 0
Question 62:
Details of ten international cricket games between two teams, "Green" and "Blue," are given in Table C. The organization would like to use this information to develop a decision-tree model to predict outcomes of future games. The computed Information Gain InformationGain(C, Pitch) with respect to the Target is:
| Match Number | Pitch | Format | Winner (Target) |
|---|---|---|---|
| 1 | S | T | Green |
| 2 | S | T | Blue |
| 3 | F | O | Blue |
| 4 | F | O | Blue |
| 5 | F | T | Green |
| 6 | F | O | Blue |
| 7 | S | O | Green |
| 8 | F | S | Blue |
| 9 | F | O | Blue |
| 10 | S | O | Green |
View Solution
Solution: The data in Table C is as follows:
| Match Number | Pitch | Format | Winner (Target) |
|---|---|---|---|
| 1 | S | T | Green |
| 2 | S | T | Blue |
| 3 | F | O | Blue |
| 4 | F | O | Blue |
| 5 | F | T | Green |
| 6 | F | O | Blue |
| 7 | S | O | Green |
| 8 | F | S | Blue |
| 9 | F | O | Blue |
| 10 | S | O | Green |
To calculate Information Gain, we need to compute the entropy of the system with respect to the Pitch attribute.
1. Entropy Calculation:
- Total entropy H(C) is calculated based on the target variable (Winner): - Total number of matches: 10 - Green wins: 4, Blue wins: 6 - The entropy is: H(C) = -( 4⁄10 log2 4⁄10 + 6⁄10 log2 6⁄10)
H(C) = - (0.4 log2 0.4 + 0.6 log2 0.6)
H(C) ≈ 0.971
2. Entropy for Each Split Based on Pitch (S and F):
- For Pitch = S: - Number of matches: 4 - Green wins: 2, Blue wins: 2 - Entropy for Pitch = S:
H(S) = -(2⁄4 log2 2⁄4 + 2⁄4 log2 2⁄4) = 1
- For Pitch = F: - Number of matches: 6 - Green wins: 2, Blue wins: 4 - Entropy for Pitch = F:
H(F) = - (2⁄6 log2 2⁄6 + 4⁄6 log2 4⁄6)
H(F) ≈ 0.918
3. Information Gain Calculation:
The information gain is calculated as:
InformationGain(C, Pitch) = H(C) - (4⁄10H(S) + 6⁄10H(F))
InformationGain(C, Pitch) = 0.971 - (4⁄10*1 + 6⁄10*0.918)
InformationGain(C, Pitch) ≈ 0.971 – (0.4 + 0.5508) = 0.971 – 0.9508 = 0.0202
Final Answer: The Information Gain InformationGain(C, Pitch) is approximately 0.02 (rounded off to two decimal places).
Question 63:
Given the two-dimensional dataset consisting of 5 data points from two classes (circles and squares) and assuming that the Euclidean distance is used to measure the distance between two points, the minimum odd value of k in the k-nearest neighbor algorithm for which the diamond (◊) shaped data point is assigned the label "square" is:
View Solution
Solution: We need to find the minimum odd value of k for which the k-nearest neighbor algorithm assigns the label "square" to the diamond (◊) shaped data point.
1. Understanding the k-Nearest Neighbor Algorithm: - In k-nearest neighbor (k-NN) classification, the label of a data point is assigned based on the majority class among the k nearest neighbors (based on Euclidean distance in this case). - We are given a dataset with 5 data points from two classes: circles and squares.
2. Properties of the k-Nearest Neighbor Algorithm: - To make sure that the classification is based on a majority vote, the value of k must be odd. This avoids ties when there is an equal number of data points from each class among the nearest neighbors.
3. Assigning the Label "Square": - The task asks for the minimum odd value of k that results in the "diamond" shaped data point being classified as a "square." - The value of k must be chosen such that the number of "square" labels among the k nearest neighbors is greater than the number of "circle" labels.
4. Conclusion: - Since we are looking for the smallest odd value of k, and there are 5 data points, the smallest odd value for k would be k = 3. For k = 3, the 3 nearest neighbors are likely to influence the classification based on the majority label among them.
k = 3
Question 64:
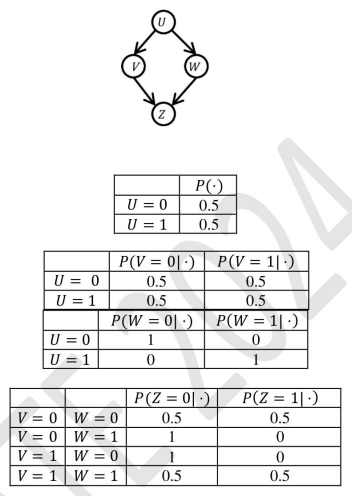
Given the following Bayesian Network consisting of four Bernoulli random variables and their associated conditional probability tables (CPTs), we need to compute P(U = 1, V = 1, W = 1, Z = 1).
View Solution
Solution: From the structure of the Bayesian Network and the conditional probability tables:
- P(U = 1) = 0.5 - P(V = 0|U = 0) = 0.5, P(V = 1|U = 0) = 0.5 - P(V = 0|U = 1) = 0.5, P(V = 1|U = 1) = 0.5 - P(W = 0|U = 0) = 1, P(W = 1|U = 0) = 0 - P(W = 0|U = 1) = 0, P(W = 1|U = 1) = 1 - P(Z = 0|V = 0, W = 0) = 0.5, P(Z = 1|V = 0,W = 0) = 0.5 - P(Z = 0|V = 0, W = 1) = 1, P(Z = 1|V = 0, W = 1) = 0 - P(Z = 0|V = 1, W = 0) = 1, P(Z = 1|V = 1, W = 0) = 0 - P(Z = 0|V = 1, W = 1) = 0.5, P(Z = 1|V = 1, W = 1) = 0.5
The goal is to compute P(U = 1, V = 1, W = 1, Z = 1).
We can break this down using the chain rule for Bayesian networks:
P(U = 1, V = 1, W = 1, Z = 1) = P(U = 1)⋅P(V = 1|U = 1)⋅P(W = 1|U = 1)⋅P(Z = 1|V = 1, W = 1)
Substitute the values from the given probabilities:
P(U = 1) = 0.5, P(V = 1|U = 1) = 0.5, P(W = 1|U = 1) = 1, P(Z = 1|V = 1, W = 1) = 0.5
Now, multiplying these together:
P(U = 1, V = 1, W = 1, Z = 1) = 0.5 × 0.5 × 1 × 0.
Solution: Given the matrix M = uuT, where u = 1⁄3, we can calculate the singular values of the matrix. The singular values of a matrix M are the square roots of the eigenvalues of the matrix MTM or MMT.
1. Matrix Calculation:
First, calculate M = uuT:
M = 1⁄3(1 3) = 1 3⁄3 9
2. Singular Values:
The matrix M is a 2 × 2 matrix. To find its singular values, we calculate the eigenvalues of MMT.
MMT = 1 3⁄3 9 * (1 3⁄3 9) = 10 30⁄30 90
To find the eigenvalues, solve the characteristic equation det (MMT – λI) = 0:
det(10 - λ 30⁄30 90-λ) = (10 - λ)(90 - λ) – 302 = 0
λ2 – 100λ = 0
λ(λ – 100) = 0
Thus, the eigenvalues are λ1 = 0 and λ2 = 100. The singular values of M are the square roots of the eigenvalues:
σ1 = √100 = 10, σ2 = 0
3. Final Answer:
Since the product of singular values is σ1·σ2, we have:
σ1σ2 = 10 × 0 = 0
Final Answer: 0
Question 62:
Details of ten international cricket games between two teams, "Green" and "Blue," are given in Table C. The organization would like to use this information to develop a decision-tree model to predict outcomes of future games. The computed Information Gain InformationGain(C, Pitch) with respect to the Target is:
| Match Number | Pitch | Format | Winner (Target) |
|---|---|---|---|
| 1 | S | T | Green |
| 2 | S | T | Blue |
| 3 | F | O | Blue |
| 4 | F | O | Blue |
| 5 | F | T | Green |
| 6 | F | O | Blue |
| 7 | S | O | Green |
| 8 | F | S | Blue |
| 9 | F | O | Blue |
| 10 | S | O | Green |
View Solution
Solution: The data in Table C is as follows:
| Match Number | Pitch | Format | Winner (Target) |
|---|---|---|---|
| 1 | S | T | Green |
| 2 | S | T | Blue |
| 3 | F | O | Blue |
| 4 | F | O | Blue |
| 5 | F | T | Green |
| 6 | F | O | Blue |
| 7 | S | O | Green |
| 8 | F | S | Blue |
| 9 | F | O | Blue |
| 10 | S | O | Green |
1. Entropy Calculation:
- Total entropy H(C) is calculated based on the target variable (Winner): - Total number of matches: 10 - Green wins: 4, Blue wins: 6 - The entropy is: H(C) = -(4⁄10 log2 4⁄10 + 6⁄10 log2 6⁄10)
H(C) = - (0.4 log2 0.4 + 0.6 log2 0.6)
H(C) ≈ 0.971
2. Entropy for Each Split Based on Pitch (S and F):
- For Pitch = S: - Number of matches: 4 - Green wins: 2, Blue wins: 2 - Entropy for Pitch = S:
H(S) = -(2⁄4 log2 2⁄4 + 2⁄4 log2 2⁄4) = 1
- For Pitch = F: - Number of matches: 6 - Green wins: 2, Blue wins: 4 - Entropy for Pitch = F:
H(F) = - (2⁄6 log2 2⁄6 + 4⁄6 log2 4⁄6)
H(F) ≈ 0.918
3. Information Gain Calculation:
The information gain is calculated as:
InformationGain(C, Pitch) = H(C) - ( 4⁄10H(S) + 6⁄10H(F) )
InformationGain(C, Pitch) = 0.971 - ( 4⁄10*1 + 6⁄10*0.918)
InformationGain(C, Pitch) ≈ 0.971 – (0.4 + 0.5508) = 0.971 – 0.9508 = 0.0202
Final Answer: The Information Gain InformationGain(C, Pitch) is approximately 0.02 (rounded off to two decimal places).
Question 63:
Given the two-dimensional dataset consisting of 5 data points from two classes (circles and squares) and assuming that the Euclidean distance is used to measure the distance between two points, the minimum odd value of k in the k-nearest neighbor algorithm for which the diamond (◊) shaped data point is assigned the label "square" is:

View Solution
Solution: We need to find the minimum odd value of k for which the k-nearest neighbor algorithm assigns the label "square" to the diamond (◊) shaped data point.
1. Understanding the k-Nearest Neighbor Algorithm: - In k-nearest neighbor (k-NN) classification, the label of a data point is assigned based on the majority class among the k nearest neighbors (based on Euclidean distance in this case). - We are given a dataset with 5 data points from two classes: circles and squares.
2. Properties of the k-Nearest Neighbor Algorithm: - To make sure that the classification is based on a majority vote, the value of k must be odd. This avoids ties when there is an equal number of data points from each class among the nearest neighbors.
3. Assigning the Label "Square”: - The task asks for the minimum odd value of k that results in the "diamond" shaped data point being classified as a "square." - The value of k must be chosen such that the number of "square" labels among the k nearest neighbors is greater than the number of "circle" labels.
4. Conclusion: - Since we are looking for the smallest odd value of k, and there are 5 data points, the smallest odd value for k would be k = 3. For k = 3, the 3 nearest neighbors are likely to influence the classification based on the majority label among them.
k = 3
Question 64:
Given the following Bayesian Network consisting of four Bernoulli random variables and their associated conditional probability tables (CPTs), we need to compute P(U = 1, V = 1, W = 1, Z = 1).
View Solution
Solution: From the structure of the Bayesian Network and the conditional probability tables:
- P(U = 1) = 0.5 - P(V = 0|U = 0) = 0.5, P(V = 1|U = 0) = 0.5 - P(V = 0|U = 1) = 0.5, P(V = 1|U = 1) = 0.5 - P(W = 0|U = 0) = 1, P(W = 1|U = 0) = 0 - P(W = 0|U = 1) = 0, P(W = 1|U = 1) = 1 - P(Z = 0|V = 0, W = 0) = 0.5, P(Z = 1|V = 0,W = 0) = 0.5 - P(Z = 0|V = 0, W = 1) = 1, P(Z = 1|V = 0, W = 1) = 0 - P(Z = 0|V = 1, W = 0) = 1, P(Z = 1|V = 1, W = 0) = 0 - P(Z = 0|V = 1, W = 1) = 0.5, P(Z = 1|V = 1, W = 1) = 0.5
The goal is to compute P(U = 1, V = 1, W = 1, Z = 1).
We can break this down using the chain rule for Bayesian networks:
P(U = 1, V = 1, W = 1, Z = 1) = P(U = 1)⋅P(V = 1|U = 1)⋅P(W = 1|U = 1)⋅P(Z = 1|V = 1, W = 1)
Substitute the values from the given probabilities:
P(U = 1) = 0.5, P(V = 1|U = 1) = 0.5, P(W = 1|U = 1) = 1, P(Z = 1|V = 1, W = 1) = 0.5
Now, multiplying these together:
P(U = 1, V = 1, W = 1, Z = 1) = 0.5 × 0.5 × 1 × 0.5 = 0.125
Thus, the value of P(U = 1, V = 1, W = 1, Z = 1) is 0.125.
Question 65:
Two fair coins are tossed independently. Let X be a random variable that takes a value of 1 if both tosses are heads, and 0 otherwise. Let Y be a random variable that takes a value of 1 if at least one of the tosses is heads, and 0 otherwise. The value of the covariance of X and Y is:
View Solution
Solution: We need to compute the covariance between X and Y, which is given by the formula:
Cov(X, Y) = E[XY] – E[X]E[Y]
Step 1: Define the possible outcomes for the coin tosses
Since we are tossing two fair coins, the possible outcomes are:
{HH, HT, TH, TT}
Each outcome has a probability of 1⁄4.
Step 2: Compute the values of X and Y for each outcome
- For HH, both tosses are heads, so X = 1 and Y = 1. - For HT, X = 0 (since both tosses are not heads), and Y = 1 (since at least one toss is heads). - For TH, X = 0, and Y = 1. - For TT, X = 0, and Y = 0.
Step 3: Compute the expected values of X and Y
We calculate E[X] and E[Y]:
E[X] = 1⁄4(1+0+0+0) = 1⁄4
E[Y] = 1⁄4(1+1+1+0) = 3⁄4
Step 4: Compute E[XY]
Next, we calculate E[XY]:
E[XY] = 1⁄4(1⋅1+0⋅1+0⋅1+0⋅0) = 1⁄4
Step 5: Compute the covariance
Now we can compute the covariance:
Cov(X, Y) = E[XY] – E[X]E[Y]
Substitute the values:
Cov(X,Y) = 1⁄4 - (1⁄4 x 3⁄4) = 1⁄4 - 3⁄16 = 1⁄16
Thus, the value of the covariance of X and Y is: 1⁄16














































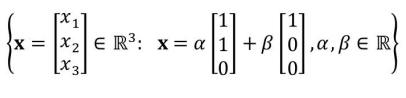
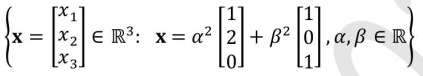

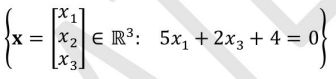

Comments