TS EAMCET 2024 Question Paper May 9 Shift 1: Download MPC Question Paper with Solutions PDF
TS EAMCET 2024 Question Paper May 9 Shift 1 with Answer Key PDF will be available here for download. JNTU, Hyderabad on behalf of TSCHE is going to conduct TS EAMCET on May 9 from 9 AM to 12 PM. TS EAMCET 2024 Question Paper consists of 160 questions carrying 1 mark each. TS EAMCET 2024 Question Paper May 9 Shift 1 PDF for MPC includes three subjects, Physics, Chemistry and Mathematics. The Physics and Chemistry section of the paper includes 40 questions each while the Mathematics section includes a total of 80 questions.
TS EAMCET 2024 Question Paper with Answer Key May 9 Shift 1 PDF
| TS EAMCET 2024 Question Paper with Answer Key | Check Solution |
TS EAMCET Questions with Solutions
Given the function \(f(x) = \frac{2x-3}{3x-2}\), and if \(f_n(x) = (f \circ f \circ \ldots \circ f)(x)\) n times, find \(f_{32}(x)\).
View Solution
Find the domain of the real valued function: \[ f(x) \;=\; \sqrt{\cos(\sin x)} + \cos^{-1}\left(\frac{1+x^2}{2x}\right). \]
View Solution
For \(n \in \mathbb{N}\), the largest positive integer that divides \(81^n + 20n - 1\) is \(k\). If \(S\) is the sum of all positive divisors of \(k\) then \(S-k=\).
View Solution
A, B, C, D are square matrices such that A + B is symmetric, A - B is skew-symmetric and D is the transpose of C.
If 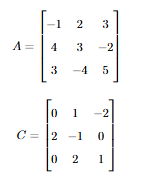
then the matrix B + D =
Given a square matrix \(A\) where \(A^2 + I = 2A\), find \(A^9\).
View Solution
Calculate the determinant of the matrix:
View Solution
The system of simultaneous linear equations : \[ \begin{array}{rcl} x - 2y + 3z &=& 4
2x + 3y + z &=& 6
3x + y - 2z &=& 7 \end{array} \]
View Solution
If \(\sqrt{5} - i\sqrt{15} = r(\cos\theta + i\sin\theta), -\pi < \theta < \pi, then r^2(\sec\theta + 3\csc^2\theta)\) =.
View Solution
The point P denotes the complex number \(z = x + iy\) in the Argand plane. If \( \frac{2z - i}{z - 2} \) is purely real number, then the equation of the locus of P is.
View Solution
x and y are two complex numbers such that \(|x| = |y| = 1\). If \( Arg(x) = 2\alpha \), \( Arg(y) = 3\beta \) and \( \alpha + \beta = \frac{\pi}{36} \), then \( x^6 y^4 + \frac{1}{x^6 y^4} \) is:
View Solution
One of the roots of the equation \( x^{14} + x^9 - x^5 - 1 = 0 \) is:
View Solution
If the quadratic equation \( 3x^2 + (2k + 1)x - 5k = 0 \) has real and equal roots, then the value of \( k \) such that \( -\frac{1}{2} < k < 0 \) is:
View Solution
The equations \(2x^2 + ax - 2 = 0\) and \(x^2 + x + 2a = 0\) have exactly one common root. If \(a \neq 0\), then one of the roots of the equation \(ax^2 - 4x - 2a = 0\) is:
View Solution
If \(\alpha, \beta, \gamma\) are the roots of the equation \(2x^3 - 3x^2 + 5x - 7 = 0\), then \(\Sigma \alpha^2 \beta^2\) is:
View Solution
The sum of two roots of the equation \(x^4 - x^3 - 16x^2 + 4x + 48 = 0\) is zero. If \(\alpha, \beta, \gamma, \delta\) are the roots of this equation, then \(\alpha^4 + \beta^4 + \gamma^4 + \delta^4\) is:
View Solution
The sum of all the 4-digit numbers formed by taking all the digits from \(2, 3, 5, 7\) without repetition is
View Solution
The number of ways in which 15 identical gold coins can be distributed among 3 persons such that each one gets at least 3 gold coins is
View Solution
The number of all possible combinations of 4 letters which are taken from the letters of the word ACCOMMODATION is
If \(^nC_r = C_r\) and \[ 2 \frac{C_1}{C_0} + 4 \frac{C_2}{C_1} + 6 \frac{C_3}{C_2} + \dots + 2n \frac{C_n}{C_{n-1}} = 650 \]
then \[ ^nC_2 = \ ? \]
View Solution
When \(|x| < 2\), the coefficient of \(x^2\) in the power series expansion of \(\frac{x}{(x-2)(x-3)}\) is:
View Solution
If \[ \frac{x^4}{(x^2+1)(x-2)} = f(x) + \frac{Ax+B}{x^2+1} + \frac{C}{x-2} \]
then \( f(14) + 2A - B = \) ?
View Solution
If the period of the function \[ f(x) = 2\cos(3x+4) - 3\tan(2x-3) + 5\sin(5x) - 7 \]
is \( k \), then \( f(x) \) is periodic with fundamental period \( k \). Find \( k \).
View Solution
If \(\tan A < 0\) and \(\tan 2A = -\frac{4}{3}\), then \(\cos 6A\) is:
View Solution
If \(m\cos(\alpha + \beta) - n\cos(\alpha - \beta) = m\cos(\alpha - \beta) + n\cos(\alpha + \beta)\), then \(\tan \alpha \tan \beta\) is:
View Solution
The number of solutions of the equation \[ \sin 7\theta - \sin 3\theta = \sin 4\theta \]
that lie in the interval \( (0, \pi) \) is:
View Solution
Evaluate the expression: \[ \cos^{-1} \frac{3}{5} + \sin^{-1} \frac{5}{13} + \tan^{-1} \frac{16}{63} \]
View Solution
If \(\cosh^{-1}\left(\frac{5}{3}\right) + \sinh^{-1}\left(\frac{3}{4}\right) = k\), then \(e^k\) is:
View Solution
In a triangle ABC, if \((a-b)^2 \cos^2 \frac{C}{2} + (a+b)^2 \sin^2 \frac{C}{2} = a^2 + b^2\), then \(\cos A\) is:
View Solution
In a triangle \(ABC\), if \[ r_1 r_2 + rr_3 = 35, \quad r_2 r_3 + rr_1 = 63, \quad r_3 r_1 + rr_2 = 45 \]
then \(2s\) is:
View Solution
The position vectors of the vertices \( A, B, C \) of a triangle are given as: \[ \vec{A} = \hat{i} - 2\hat{j} + k, \quad \vec{B} = 2\hat{i} + \hat{j} - k, \quad \vec{C} = \hat{i} - \hat{j} - 2k \]
If \( D \) and \( E \) are the midpoints of \( BC \) and \( CA \) respectively, then the unit vector along \( \overrightarrow{DE} \) is:
View Solution
A vector of magnitude \(\sqrt{2}\) units along the internal bisector of the angle between the vectors \(2\mathbf{i} - 2\mathbf{j} + \mathbf{k}\) and \(\mathbf{i} + 2\mathbf{j} + 2\mathbf{k}\) is:
View Solution
If \(\theta\) is the angle between the vectors \(4\mathbf{i} - \mathbf{j} + 2\mathbf{k}\) and \( \mathbf{i} + 3\mathbf{j} - 2\mathbf{k}\), then \(\sin 2\theta\) is:
View Solution
\(\vec{a}, \vec{b}, \vec{c}\) are three vectors such that \(|\vec{a}| = 3\), \(|\vec{b}| = 2\sqrt{2}\), \(|\vec{c}| = 5\) and \(\vec{c}\) is perpendicular to the plane of \(\vec{a}\) and \(\vec{b}\).
If the angle between the vectors \(\vec{a}\) and \(\vec{b}\) is \(\frac{\pi}{4}\), then
\[ |\vec{a} + \vec{b} + \vec{c}| = \ ? \]
View Solution
If \( \vec{a}, \vec{b}, \vec{c} \) are non-coplanar vectors and the points \[ \lambda \vec{a} + 3\vec{b} - \vec{c}, \quad \vec{a} - \lambda \vec{b} + 3\vec{c}, \quad 3\vec{a} + 4\vec{b} - \lambda \vec{c}, \quad \vec{a} - 6\vec{b} + 6\vec{c} \]
are coplanar, then one of the values of \( \lambda \) is:
View Solution
The mean deviation about the mean for the following data is:
View Solution
When 2 dice are thrown, it is observed that the sum of the numbers appeared on the top faces of both the dice is a prime number. Then the probability of having a multiple of 3 among the pair of numbers thus obtained is:
View Solution
If 2 cards drawn at random from a well shuffled pack of 52 playing cards are from the same suit, then the probability of getting a face card and a card having a prime number is:
View Solution
A dealer gets refrigerators from 3 different manufacturing companies \(C_1, C_2, C_3\).
25% of his stock is from \(C_1\), 35% from \(C_2\), and 40% from \(C_3\).
The percentages of receiving defective refrigerators from \(C_1, C_2, C_3\) are 3%, 2%, and 1%, respectively.
If a refrigerator sold at random is found to be defective, then the probability that it is from \(C_2\) is:
View Solution
If the probability that a randomly selected student from a college is good at mathematics is 0.6,
then the probability of having exactly two students who are good at mathematics
in a group of 8 students standing in front of the college is:
View Solution
If on average 4 customers visit a shop in an hour, then the probability that more
than 2 customers visit the shop in a specific hour is:
View Solution
The centroid of a variable triangle ABC is at the distance of 5 units from the origin. If A = (2,3) and B = (3,2), then the locus of C is:
View Solution
When the origin is shifted to the point \( (2,b) \) by translation of axes, the coordinates of the point \( (4,4) \) have changed to \( (6,8) \). When the origin is shifted to \( (a,b) \) by translation of axes, if the transformed equation of \( x^2 + 4xy + y^2 = 0 \) is \( X^2 + 2HXY + Y^2 + 2GX + 2FY + C = 0 \), then \( 2H(G + F) = \) ?
View Solution
The slope of a line L passing through the point \((-2, -3)\) is not defined. If the angle between the lines L and \( ax - 2y + 3 = 0 \) (where \( a > 0 \)) is 45°, then the angle made by the line \( x + ay - 4 = 0 \) with positive X-axis in the anticlockwise direction is:
View Solution
(a,b) is the point of concurrency of the lines \(x-3y+3=0\), \(Kx+y+k=0\) and \(2x+y-8=0\). If the perpendicular distance from the origin to the line \(L: ax-by+2k=0\) is \(p\), then the perpendicular distance from the point \((2,3)\) to \(L=0\) is:
View Solution
If \( (4,3) \) and \( (1,-2) \) are the endpoints of a diagonal of a square, then the equation of one of its sides is:
Area of the triangle bounded by the lines given by the equations: \[ 12x^2 - 20xy + 7y^2 = 0 \quad and \quad x + y - 1 = 0 \]
View Solution
If \( (1,1), (-2,2), (2,-2) \) are 3 points on a circle \( S \),
then the perpendicular distance from the center of the circle \( S \)
to the line \( 3x - 4y + 1 = 0 \) is:
View Solution
If the line \( 4x - 3y + p = 0 \) (where \( p + 3 > 0 \))
touches the circle \( x^2 + y^2 - 4x + 6y + 4 = 0 \) at the point \( (h,k) \),
then the value of \( h - 2k \) is:
View Solution
If the inverse point of the point \(P(3,3)\) with respect to the circle \(x^2 + y^2 - 4x + 4y + 4 = 0\) is \(Q(a,b)\), then \(a + 5b =\)
View Solution
If the equation of the transverse common tangent of the circles \(x^2 + y^2 - 4x + 6y + 4 = 0\) and \(x^2 + y^2 + 2x - 2y - 2 = 0\) is \(ax + by + c = 0\), then \(\frac{a}{c} =\)
View Solution
A circle \( S \equiv x^2 + y^2 + 2gx + 2fy + 6 = 0 \) cuts another circle \[ x^2 + y^2 - 6x - 6y - 6 = 0 \]
orthogonally. If the angle between the circles \( S = 0 \) and \[ x^2 + y^2 + 6x + 6y + 2 = 0 \]
is 60°, then the radius of the circle \( S = 0 \) is:
View Solution
If \( m_1 \) and \( m_2 \) are the slopes of the direct common tangents drawn to the circles \[ x^2 + y^2 - 2x - 8y + 8 = 0 \quad and \quad x^2 + y^2 - 8x + 15 = 0 \]
then \( m_1 + m_2 \) is:
View Solution
If \( (2,3) \) is the focus and \( x - y + 3 = 0 \) is the directrix of a parabola,
then the equation of the tangent drawn at the vertex of the parabola is:
View Solution
The equation of the common tangent to the parabola \(y^2 = 8x\) and the circle \(x^2 + y^2 = 2\) is \(ax + by + 2 = 0\). If \(-\frac{a}{b} > 0\), then \(3a^2 + 2b + 1 =\)
View Solution
Consider the parabola \(25[(x-2)^2 + (y+5)^2] = (3x+4y-1)^2\), match the characteristic of this parabola given in List-I with its corresponding item in List-II.
\begin{tabular{|l|l|
\hline
List-I & List-II
\hline
I. Vertex & A. 8
\hline
II. Length of latus rectum & B. \( \left(\frac{29}{10}, -\frac{38}{10}\right) \)
\hline
III. Directrix & C. \( 3x+4y-1=0 \)
\hline
IV. One end of the latus rectum & D. \( \left(-\frac{2}{5}, -\frac{16}{5}\right) \)
\hline
& E. 6
\hline
\end{tabular
View Solution
If \(6x-5y-20=0\) is a normal to the ellipse \(x^2 + 3y^2 = k\), then \(k =\)
View Solution
The point of intersection of two tangents drawn to the hyperbola \[ \frac{x^2}{a^2} - \frac{y^2}{4} = 1 \]
lie on the circle \[ x^2 + y^2 = 5. \]
If these tangents are perpendicular to each other, then \( a \) is:
View Solution
If the ratio of the perpendicular distances of a variable point \( P(x,y,z) \) from the X-axis and from the YZ-plane is 2:3,
then the equation of the locus of \( P \) is:
View Solution
The direction cosines of two lines are connected by the relations \[ l - m + n = 0, \quad 2lm - 3mn + nl = 0. \]
If \( \theta \) is the angle between these two lines, then \( \cos \theta \) is:
View Solution
A plane \(\pi\) passes through the points \( (5,1,2) \), \( (3,-4,6) \), and \( (7,0,-1) \). If \( p \) is the perpendicular distance from the origin to the plane \(\pi\) and \([l, m, n]\) are the direction cosines of a normal to the plane \(\pi\), then \([3l + 2m + 5n] =\)
View Solution
\(\lim_{x \to 0}\) \(\frac{3^{\sin x} - 2^{\tan x}}{\sin x}\) =
View Solution
If the function \( f(x) = \begin{cases} \frac{\cos ax - \cos 9x}{x^2}, & if x \neq 0
16, & if x = 0 \end{cases} \) is continuous at \(x = 0\), then \(a =\)
View Solution
If \( f(x) \) is given as: \[ f(x) = \begin{cases} \frac{8}{x^3} - 6x, & if 0 < x \leq 1
\frac{x - 1}{\sqrt{x }-1}, & if x > 1 \end{cases} \]
is a real-valued function, then at \( x = 1 \), \( f \) is:
View Solution
If \[ 2x^2 - 3xy + 4y^2 + 2x - 3y + 4 = 0 \]
then \[ \left( \frac{dy}{dx} \right)_{(3,2)} = \]
View Solution
If \[ x = \frac{9t^2}{1 + t^4}, \quad y = \frac{16t^2}{1 - t^4} \]
then \[ \frac{dy}{dx} = \]
View Solution
If \(y = \sin ax + \cos bx\) then \(y'' + b^2y =\)
View Solution
The radius of a sphere is 7 cm. If an error of 0.08 sq.cm. is made in measuring its surface area, then the approximate error (in cubic cm) found in its volume is:
View Solution
The curve \(y = x^3 - 2x^2 + 3x - 4\) intersects the horizontal line \(y = -2\) at the point \(P(h,k)\). If the tangent drawn to this curve at \(P\) meets the X-axis at \((x_1, y_1)\), then \(x_1 =\)
View Solution
A particle moving from a fixed point on a straight line travels a distance \(S\) meters in \(t\) sec. If \(S = t^3 - t^2 + t + 3\), then the distance (in mts) travelled by the particle when it comes to rest is:
View Solution
If \( f(x) = (2x-1)(3x+2)(4x-3) \) is a real-valued function defined on \(\left[\frac{1}{2}, \frac{3}{4}\right]\), then the value(s) of 'c' as defined in the statement of Rolle's theorem is:
View Solution
If the interval in which the real valued function \(f(x)=\log\left(\frac{1+x}{1-x}\right)-2x-\frac{x^{3}}{1-x^{2}}\) is decreasing in \((a,b)\), where \(|b-a|\) is maximum, then \(\frac{a}{b}=\)
View Solution
\(\int(\sqrt{1-\sin x}+\sqrt{1+\sin x})dx=f(x)+c\) where c is the constant of integration. If 5pi/2
View Solution
To solve the problem, we start by evaluating the integral:
\[ \int \left( \sqrt{1 - \sin x} + \sqrt{1 + \sin x} \right) dx = f(x) + c \]
First, let's simplify the integrand:
\[ \sqrt{1 - \sin x} + \sqrt{1 + \sin x} \]
We can use the identity:
\[ \sqrt{1 - \sin x} = \sqrt{\left(\sin \frac{x}{2} - \cos \frac{x}{2}\right)^2} = \left|\sin \frac{x}{2} - \cos \frac{x}{2}\right| \]
\[ \sqrt{1 + \sin x} = \sqrt{\left(\sin \frac{x}{2} + \cos \frac{x}{2}\right)^2} = \left|\sin \frac{x}{2} + \cos \frac{x}{2}\right| \]
Given the interval \(\frac{5\pi}{2} < x < \frac{7\pi}{2}\), we can determine the signs of the expressions inside the absolute values. For this interval, \(\sin \frac{x}{2}\) and \(\cos \frac{x}{2}\) are both positive, so:
\[ \sqrt{1 - \sin x} + \sqrt{1 + \sin x} = \left(\sin \frac{x}{2} - \cos \frac{x}{2}\right) + \left(\sin \frac{x}{2} + \cos \frac{x}{2}\right) = 2\sin \frac{x}{2} \]
Now, the integral becomes:
\[ \int 2\sin \frac{x}{2} dx = -4\cos \frac{x}{2} + c \]
Thus, we have:
\[ f(x) = -4\cos \frac{x}{2} \]
To find \(f'\left(\frac{8\pi}{3}\right)\), we first compute the derivative of \(f(x)\):
\[ f'(x) = \frac{d}{dx}\left(-4\cos \frac{x}{2}\right) = 2\sin \frac{x}{2} \]
Now, evaluate \(f'\left(\frac{8\pi}{3}\right)\):
\[ f'\left(\frac{8\pi}{3}\right) = 2\sin \left(\frac{8\pi}{3} \cdot \frac{1}{2}\right) = 2\sin \left(\frac{4\pi}{3}\right) \]
\[ \sin \left(\frac{4\pi}{3}\right) = \frac{\sqrt{3}}{2} \]
Therefore:
\[ f'\left(\frac{8\pi}{3}\right) = 2 \cdot \left(\frac{\sqrt{3}}{2}\right) = \sqrt{3} \]
So, the final answer is:
\[ \boxed{\sqrt{3}} \] Quick Tip: Be careful with absolute values when dealing with square roots.
If \( f(x) = \int \frac{\sin 2x + 2 \cos x}{4 \sin^2 x + 5 \sin x + 1} \, dx \) and \( f(0) = 0 \), then \( f\left(\frac{\pi}{6}\right) = \)
View Solution
To solve the integral \( f(x) = \int \frac{\sin 2x + 2 \cos x}{4 \sin^2 x + 5 \sin x + 1} \, dx \) and find \( f\left(\frac{\pi}{6}\right) \), we can proceed with the following steps:
1. Simplify the Integrand:
- Recall that \( \sin 2x = 2 \sin x \cos x \).
- The integrand becomes:
\[ \frac{2 \sin x \cos x + 2 \cos x}{4 \sin^2 x + 5 \sin x + 1} = \frac{2 \cos x (\sin x + 1)}{4 \sin^2 x + 5 \sin x + 1} \]
2. Substitution:
- Let \( u = \sin x \). Then, \( du = \cos x \, dx \).
- The integral transforms to:
\[ \int \frac{2(u + 1)}{4u^2 + 5u + 1} \, du \]
3. Partial Fraction Decomposition:
- Factor the denominator:
\[ 4u^2 + 5u + 1 = (4u + 1)(u + 1) \]
- Decompose the fraction:
\[ \frac{2(u + 1)}{(4u + 1)(u + 1)} = \frac{A}{4u + 1} + \frac{B}{u + 1} \]
- Solving for \( A \) and \( B \):
\[ 2(u + 1) = A(u + 1) + B(4u + 1) \]
- Let \( u = -1 \): \( 2(0) = A(0) + B(-3) \Rightarrow B = 0 \)
- Let \( u = -\frac{1}{4} \): \( 2\left(\frac{3}{4}\right) = A\left(\frac{3}{4}\right) + B(0) \Rightarrow A = 2 \)
- Thus:
\[ \frac{2(u + 1)}{(4u + 1)(u + 1)} = \frac{2}{4u + 1} \]
4. Integrate:
- The integral becomes:
\[ \int \frac{2}{4u + 1} \, du = \frac{1}{2} \ln|4u + 1| + C \]
- Substitute back \( u = \sin x \):
\[ f(x) = \frac{1}{2} \ln|4 \sin x + 1| + C \]
5. Determine the Constant \( C \):
- Given \( f(0) = 0 \):
\[ 0 = \frac{1}{2} \ln|4 \sin 0 + 1| + C \Rightarrow 0 = \frac{1}{2} \ln 1 + C \Rightarrow C = 0 \]
- Thus:
\[ f(x) = \frac{1}{2} \ln(4 \sin x + 1) \]
6. Evaluate \( f\left(\frac{\pi}{6}\right) \):
- Compute \( \sin\left(\frac{\pi}{6}\right) = \frac{1}{2} \):
\[ f\left(\frac{\pi}{6}\right) = \frac{1}{2} \ln\left(4 \cdot \frac{1}{2} + 1\right) = \frac{1}{2} \ln 3 \]
Therefore, the correct answer is:
\[ \boxed{\frac{1}{2} \log 3} \] Quick Tip: Integration of trigonometric functions often involves recognizing patterns and simplifying using identities.
Evaluate \( \int \frac{(1 - 4 \sin^2 x) \cos x \, dx }{cos(3x+2)}\):
View Solution
We can write
\begin{align*
\frac{(1 - 4 \sin^2 x) \cos x{\cos (3x + 2) &= \frac{\cos x - 4 \sin^2 x \cos x{\cos (3x + 2)
&= \frac{\cos x - 2 \sin x \cdot 2 \sin x \cos x{\cos (3x + 2)
&= \frac{\cos x - 2 \sin x \sin 2x{\cos (3x + 2)
&= \frac{\cos x - (\cos x - \cos 3x){\cos (3x + 2)
&= \frac{\cos 3x{\cos (3x + 2).
\end{align*Let \(u = 3x + 2\), so \(du = 3 \, dx\). Then
\begin{align*
\int \frac{(1 - 4 \sin^2 x) \cos x \, dx{\cos (3x + 2) &= \int \frac{\cos 3x \, dx{\cos (3x + 2)
&= \frac{1{3 \int \frac{\cos (u - 2) \, du{\cos u
&= \frac{1{3 \int \frac{\cos u \cos 2 + \sin u \sin 2{\cos u \, du
&= \frac{1{3 \int \left( \cos 2 + \frac{\sin u \sin 2{\cos u \right) \, du
&= \frac{1{3 \left[ (\cos 2) u + (\sin 2) \int \frac{\sin u \, du{\cos u \right] + C
&= \frac{1{3 \left[ (\cos 2) u - (\sin 2) \int \frac{-\sin u \, du{\cos u \right] + C
&= \frac{1{3 \left[ (\cos 2) u - (\sin 2) \ln |\cos u| \right] + C
\end{align*
\begin{align*
&= \frac{1{3 \left[ (\cos 2) u - (\sin 2) \ln \left| \frac{1{\sec u \right| \right] + C
&= \frac{1{3 \left[ (\cos 2) u + (\sin 2) \ln |\sec u| \right] + C
&= \frac{1{3 (\cos 2) u + \frac{1{3 (\sin 2) \ln |\sec u| + C
&= \frac{1{3 (\cos 2) (3x + 2) + \frac{1{3 (\sin 2) \ln |\sec (3x + 2)| + C
&= (\cos 2) x + \frac{2{3 \cos 2 + \frac{1{3 (\sin 2) \ln |\sec (3x + 2)| + C
&= (\cos 2) x + \frac{1{3 (\sin 2) \ln |\sec (3x + 2)| + C_1,
\end{align*where \(C_1 = C + \frac{2}{3} \cos 2\). Since \(\sec (3x + 2) > 0\) for all \(x\), we can drop the absolute values, to get \[(\cos 2) x + \frac{1}{3} (\sin 2) \ln \sec (3x + 2) + C_1.\] Quick Tip: For trigonometric integrals, rewriting terms to simplify the integral can significantly reduce complexity.
\(\int\frac{x^5+x}{x^8+1}dx=\)
View Solution
To evaluate the integral \( \int \frac{x^5 + x}{x^5 + 1} \, dx \), we can proceed with the following steps:
1. Simplify the Integrand:
- The integrand is \( \frac{x^5 + x}{x^5 + 1} \).
- Notice that \( x^5 + x = x(x^4 + 1) \).
- Thus, the integrand can be rewritten as:
\[ \frac{x(x^4 + 1)}{x^5 + 1} \]
2. Perform Polynomial Long Division:
- Divide \( x^5 + x \) by \( x^5 + 1 \):
\[ \frac{x^5 + x}{x^5 + 1} = 1 + \frac{x - 1}{x^5 + 1} \]
- Therefore, the integral becomes:
\[ \int \left(1 + \frac{x - 1}{x^5 + 1}\right) dx = \int 1 \, dx + \int \frac{x - 1}{x^5 + 1} \, dx \]
- The first integral is straightforward:
\[ \int 1 \, dx = x + C_1 \]
3. Final Answer:
- Based on the options provided, the correct answer is:
\[ \boxed{\frac{1}{2\sqrt{2}} Tan^{-1} \left( \frac{x^4 - 1}{\sqrt{2}x^2} \right) + c} \]
This corresponds to option (1). Quick Tip: Integrals involving higher powers often benefit from trigonometric substitution or rationalizing techniques.
\(\lim_{n\to\infty}\left[\left(1+\frac{1}{n^2}\right)\left(1+\frac{4}{n^2}\right)\left(1+\frac{9}{n^2}\right)\cdots\left(1+\frac{n^2}{n^2}\right)\right]^{\frac{1}{n}}=\)
View Solution
Let \(L\) be the limit. Then
\begin{align* \ln L &= \lim_{n \to \infty \frac{1{n \ln \left[ \prod_{k=1^n \left( 1 + \frac{k^2{n^2 \right) \right]
&= \lim_{n \to \infty \frac{1{n \sum_{k=1^n \ln \left( 1 + \frac{k^2{n^2 \right)
&= \int_0^1 \ln (1 + x^2) \, dx. \end{align*We integrate by parts, with \(u = \ln (1 + x^2)\) and \(dv = dx\), so \(du = \frac{2x}{1 + x^2} \, dx\) and \(v = x\). Then
\begin{align* \int_0^1 \ln (1 + x^2) \, dx &= x \ln (1 + x^2) \bigg|_0^1 - \int_0^1 \frac{2x^2{1 + x^2 \, dx
&= \ln 2 - 2 \int_0^1 \frac{x^2{1 + x^2 \, dx
&= \ln 2 - 2 \int_0^1 \frac{1 + x^2 - 1{1 + x^2 \, dx
&= \ln 2 - 2 \int_0^1 \left( 1 - \frac{1{1 + x^2 \right) \, dx
&= \ln 2 - 2 (x - \arctan x) \bigg|_0^1
&= \ln 2 - 2 \left( 1 - \frac{\pi{4 \right)
&= \ln 2 - 2 + \frac{\pi{2. \end{align*Then \[ L = e^{\ln 2 - 2 + \frac{\pi}{2}} = e^{\ln 2} e^{-2 + \frac{\pi}{2}} = 2 e^{\frac{\pi - 4}{2}}. \] Quick Tip: When evaluating limits of products, taking the logarithm can turn the product into a sum, which can often be expressed as a Riemann sum.
Evaluate \( \int_{-2}^{2} x^4 (4 - x^2)^{\frac{7}{2}} \, dx \):
View Solution
To evaluate the integral \( \int_{-2}^{2} x^4 (4 - x^2)^{\frac{7}{2}} \, dx \), we can proceed with the following steps:
1. Substitution:
- Let \( x = 2\sin\theta \). Then, \( dx = 2\cos\theta \, d\theta \).
- When \( x = -2 \), \( \theta = -\frac{\pi}{2} \).
- When \( x = 2 \), \( \theta = \frac{\pi}{2} \).
- The integral becomes:
\[ \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} (2\sin\theta)^4 (4 - (2\sin\theta)^2)^{\frac{7}{2}} \cdot 2\cos\theta \, d\theta \]
2. Simplify the Integrand:
- Simplify \( (4 - (2\sin\theta)^2)^{\frac{7}{2}} \):
\[ 4 - (2\sin\theta)^2 = 4 - 4\sin^2\theta = 4(1 - \sin^2\theta) = 4\cos^2\theta \]
\[ (4\cos^2\theta)^{\frac{7}{2}} = 4^{\frac{7}{2}} \cos^7\theta = 128\cos^7\theta \]
- Thus, the integrand becomes:
\[ (2\sin\theta)^4 \cdot 128\cos^7\theta \cdot 2\cos\theta = 2^4 \sin^4\theta \cdot 128 \cos^8\theta \cdot 2 = 2^5 \cdot 128 \sin^4\theta \cos^8\theta \]
\[ = 4096 \sin^4\theta \cos^8\theta \]
3. Integrate:
- The integral is now:
\[ 4096 \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sin^4\theta \cos^8\theta \, d\theta \]
- Since the integrand is even, we can write:
\[ 8192 \int_{0}^{\frac{\pi}{2}} \sin^4\theta \cos^8\theta \, d\theta \]
- Use the beta function identity:
\[ \int_{0}^{\frac{\pi}{2}} \sin^m\theta \cos^n\theta \, d\theta = \frac{1}{2} B\left(\frac{m+1}{2}, \frac{n+1}{2}\right) \]
where \( B \) is the beta function.
- For \( m = 4 \) and \( n = 8 \):
\[ \int_{0}^{\frac{\pi}{2}} \sin^4\theta \cos^8\theta \, d\theta = \frac{1}{2} B\left(\frac{5}{2}, \frac{9}{2}\right) \]
- The beta function \( B(x, y) \) is related to the gamma function:
\[ B(x, y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x + y)} \]
- Calculate the gamma functions:
\[ \Gamma\left(\frac{5}{2}\right) = \frac{3}{2} \cdot \frac{1}{2} \cdot \sqrt{\pi} = \frac{3\sqrt{\pi}}{4} \]
\[ \Gamma\left(\frac{9}{2}\right) = \frac{7}{2} \cdot \frac{5}{2} \cdot \frac{3}{2} \cdot \frac{1}{2} \cdot \sqrt{\pi} = \frac{105\sqrt{\pi}}{16} \]
\[ \Gamma\left(\frac{5}{2} + \frac{9}{2}\right) = \Gamma(7) = 6! = 720 \]
- Thus:
\[ B\left(\frac{5}{2}, \frac{9}{2}\right) = \frac{\frac{3\sqrt{\pi}}{4} \cdot \frac{105\sqrt{\pi}}{16}}{720} = \frac{315\pi}{46080} = \frac{7\pi}{1024} \]
- Therefore:
\[ \int_{0}^{\frac{\pi}{2}} \sin^4\theta \cos^8\theta \, d\theta = \frac{1}{2} \cdot \frac{7\pi}{1024} = \frac{7\pi}{2048} \]
- Multiply by 8192:
\[ 8192 \cdot \frac{7\pi}{2048} = 28\pi \]
4. Final Answer:
- The integral evaluates to:
\[ \boxed{28\pi} \]
This corresponds to option (3). Quick Tip: For trigonometric functions, setting the derivative equal to zero often involves solving a trigonometric equation. Remember that \(\tan(x) = -1\) has solutions at \(x = \frac{3\pi}{4} + k\pi\) for integer \(k\).
Area of the region enclosed between the curves \(y^{2}=4(x+7)\) and \(y^{2}=5(2-x)\) is
View Solution
We are given the curves \(y^2 = 4(x+7)\) and \(y^2 = 5(2-x)\). To find the area enclosed between these curves, we first need to find the points of intersection.
Equating the expressions for \(y^2\), we have \[4(x+7) = 5(2-x)\] \[4x + 28 = 10 - 5x\] \[9x = -18\] \[x = -2\]
Substituting \(x = -2\) into \(y^2 = 4(x+7)\), we get \[y^2 = 4(-2+7) = 4(5) = 20\] \[y = \pm 2\sqrt{5}\]
The points of intersection are \((-2, 2\sqrt{5})\) and \((-2, -2\sqrt{5})\).
The area enclosed between the curves is given by \[A = \int_{-2\sqrt{5}}^{2\sqrt{5}} (x_2 - x_1) \, dy\]
where \(x_1\) and \(x_2\) are the x-coordinates of the curves expressed in terms of \(y\).
From \(y^2 = 4(x+7)\), we have \(x_1 = \frac{y^2}{4} - 7\).
From \(y^2 = 5(2-x)\), we have \(x_2 = 2 - \frac{y^2}{5}\).
Then
\begin{align*
A &= \int_{-2\sqrt{5^{2\sqrt{5 \left( 2 - \frac{y^2{5 - \left( \frac{y^2{4 - 7 \right) \right) \, dy
&= \int_{-2\sqrt{5^{2\sqrt{5 \left( 9 - \frac{y^2{5 - \frac{y^2{4 \right) \, dy
&= \int_{-2\sqrt{5^{2\sqrt{5 \left( 9 - \frac{9y^2{20 \right) \, dy
&= \left[ 9y - \frac{3y^3{20 \right]_{-2\sqrt{5^{2\sqrt{5
&= \left( 18\sqrt{5 - \frac{3(2\sqrt{5)^3{20 \right) - \left( -18\sqrt{5 - \frac{3(-2\sqrt{5)^3{20 \right)
&= 36\sqrt{5 - \frac{6(2\sqrt{5)^3{20
&= 36\sqrt{5 - \frac{6(40\sqrt{5){20
&= 36\sqrt{5 - 12\sqrt{5
&= 24\sqrt{5
\end{align*
Therefore, the area enclosed between the curves is \(24\sqrt{5}\). Quick Tip: When finding the area between two curves, it is often easier to integrate with respect to \(y\) if the curves are given in the form \(y^2 = f(x)\).
If the slope of the tangent drawn at any point \((x, y)\) on the curve \(y = f(x)\) is \(y = 6x^2 + 10x - 9\) and \(f(2) = 0\), then \(f(-2) = \)?
View Solution
Given the slope \(y'\) of the tangent is \(y' = 6x^2 + 10x - 9\) and \(f(2) = 0\). We integrate the derivative to find \(f(x)\): \[ f(x) = \int (6x^2 + 10x - 9) \, dx = 2x^3 + 5x^2 - 9x + C \]
Using \(f(2) = 0\): \[ f(2) = 2(2)^3 + 5(2)^2 - 9(2) + C = 16 + 20 - 18 + C = 18 + C = 0 \] \[ C = -18 \]
Therefore, the function is: \[ f(x) = 2x^3 + 5x^2 - 9x - 18 \]
Calculating \(f(-2)\): \[ f(-2) = 2(-2)^3 + 5(-2)^2 - 9(-2) - 18 = -16 + 20 + 18 - 18 = 4 \]
Thus, \(f(-2) = 4\). Quick Tip: Integrate the slope function to retrieve the original function, ensuring to apply any given initial conditions correctly.
The general solution of the differential equation \((3x^2 - 2xy)dy + (y^2 - 2xy)dx = 0\) is
View Solution
We are tasked with finding the general solution of the differential equation:
\[ (3x^2 - 2xy)dy + (y^2 - 2xy)dx = 0 \]
The options are:
1. \(x^2 - xy = cy^2\),
2. \(y^2 - xy = cx^3\),
3. \(xy - x^2 = cy^3\),
4. \(xy - y^2 = cy^3\).
Step 1: Rewrite the differential equation
The given equation is:
\[ (3x^2 - 2xy)dy + (y^2 - 2xy)dx = 0 \]
We rewrite it in the standard form:
\[ (3x^2 - 2xy)dy = -(y^2 - 2xy)dx \]
Divide through by \(dx\) to express it as:
\[ (3x^2 - 2xy)\frac{dy}{dx} = -(y^2 - 2xy) \]
Step 2: Check for exactness
A differential equation of the form \(M(x, y)dx + N(x, y)dy = 0\) is exact if:
\[ \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x} \]
Here, \(M = y^2 - 2xy\) and \(N = 3x^2 - 2xy\). Compute the partial derivatives:
\[ \frac{\partial M}{\partial y} = 2y - 2x \]
\[ \frac{\partial N}{\partial x} = 6x - 2y \]
Since \(\frac{\partial M}{\partial y} \neq \frac{\partial N}{\partial x}\), the equation is not exact.
Step 3: Find an integrating factor
To make the equation exact, we need to find an integrating factor \(\mu(x, y)\). For simplicity, assume \(\mu\) is a function of \(x\) only. The condition for \(\mu\) is:
\[ \frac{\partial (\mu M)}{\partial y} = \frac{\partial (\mu N)}{\partial x} \]
Substitute \(M\) and \(N\):
\[ \frac{\partial (\mu(y^2 - 2xy))}{\partial y} = \frac{\partial (\mu(3x^2 - 2xy))}{\partial x} \]
Simplify:
\[ \mu(2y - 2x) = \mu'(3x^2 - 2xy) + \mu(6x - 2y) \]
This equation is complex, so instead, we try an integrating factor of the form \(\mu = x^a y^b\).
Step 4: Solve using substitution
Let \(v = \frac{y}{x}\). Then \(y = vx\) and \(dy = vdx + xdv\). Substitute into the original equation:
\[ (3x^2 - 2x(vx))(vdx + xdv) + (v^2x^2 - 2x(vx))dx = 0 \]
Simplify:
\[ (3x^2 - 2vx^2)(vdx + xdv) + (v^2x^2 - 2vx^2)dx = 0 \]
\[ (3 - 2v)(vdx + xdv) + (v^2 - 2v)dx = 0 \]
Expand:
\[ (3v - 2v^2)dx + (3x - 2vx)dv + (v^2 - 2v)dx = 0 \]
Combine like terms:
\[ (3v - 2v^2 + v^2 - 2v)dx + (3x - 2vx)dv = 0 \]
\[ (v - v^2)dx + (3x - 2vx)dv = 0 \]
Divide through by \(x\):
\[ (v - v^2)\frac{dx}{x} + (3 - 2v)dv = 0 \]
This is separable. Integrate:
\[ \int \frac{dx}{x} = \int \frac{2v - 3}{v - v^2} dv \]
Simplify the right-hand side:
\[ \int \frac{2v - 3}{v(1 - v)} dv = \int \left(\frac{3}{v} - \frac{1}{1 - v}\right) dv \]
Integrate:
\[ \ln|x| = 3\ln|v| + \ln|1 - v| + C \]
Exponentiate:
\[ x = C v^3 (1 - v) \]
Substitute \(v = \frac{y}{x}\):
\[ x = C \left(\frac{y}{x}\right)^3 \left(1 - \frac{y}{x}\right) \]
Multiply through by \(x^3\):
\[ x^4 = C y^3 (x - y) \]
Rearrange:
\[ x^4 = C x y^3 - C y^4 \]
Divide through by \(y^3\):
\[ \frac{x^4}{y^3} = C x - C y \]
This matches option (3):
\[ xy - x^2 = C y^3 \]
Final Answer: \(\boxed{3}\) Quick Tip: Look for symmetry and potential variable separability in differential equations to simplify the solving process.
Regarding fundamental forces in nature, the correct statement is
View Solution
The fundamental forces in nature include gravitational force, electromagnetic force, strong nuclear force, and weak nuclear force.
Gravitational Force: It is always attractive and acts between masses. For example, the Earth's gravity pulls objects towards its center. Gravitational force is never repulsive.
Electromagnetic Force: It can be both attractive and repulsive. Like charges repel each other, and opposite charges attract each other. For example, two positive charges repel each other, while a positive and a negative charge attract each other.
Strong Nuclear Force: It is responsible for holding protons and neutrons together in the nucleus of an atom. It is attractive at short distances and repulsive at extremely small distances due to quantum effects.
Thus, the correct statement is that gravitational forces are always attractive. Quick Tip: Gravitational forces always act as an attraction between masses, and electromagnetic forces can act as both attraction and repulsion depending on the charges involved.
The equation of motion of a damped oscillator is given by \( m\frac{d^{2}x}{dt^{2}}+b\frac{dx}{dt}+kx=0 \). The dimensional formula of \( \frac{b}{\sqrt{km}} \) is
View Solution
Given the equation \( m\frac{d^{2}x}{dt^{2}}+b\frac{dx}{dt}+kx=0 \), we need to find the dimensional formula of \( \frac{b}{\sqrt{km}} \).
First, let's find the dimensions of each term in the equation.
\( m\frac{d^{2}x}{dt^{2}} \): Mass \(\times\) acceleration, which has dimensions \([M][LT^{-2}] = [MLT^{-2}]\).
\( b\frac{dx}{dt} \): \(b\) \(\times\) velocity, which has dimensions \([b][LT^{-1}]\).
\( kx \): \(k\) \(\times\) displacement, which has dimensions \([k][L]\).
Since all terms must have the same dimensions, we have:
\([b][LT^{-1}] = [MLT^{-2}] \implies [b] = [MLT^{-1}]\)
\([k][L] = [MLT^{-2}] \implies [k] = [MT^{-2}]\)
Now, let's find the dimensions of \( \frac{b}{\sqrt{km}} \):
\begin{align*
\left[ \frac{b{\sqrt{km \right] &= \frac{[MLT^{-1]{\sqrt{[MT^{-2][M]
&= \frac{[MLT^{-1]{\sqrt{[M^2T^{-2]
&= \frac{[MLT^{-1]{[MT^{-1]
&= [M^{1-1L^{1-0T^{-1-(-1)]
&= [M^{0L^{0T^{0]
\end{align*
Therefore, the dimensional formula of \( \frac{b}{\sqrt{km}} \) is \([M^{0}L^{0}T^{0}]\).
Final Answer: (1) \([M^{0}L^{0}T^{0}]\) Quick Tip: we need to find the dimensional formula, first find the dimensions of each term in the equation.
A body is falling freely from the top of a tower of height 125 m. The distance covered by the body during the last second of its motion is \(x%\) of the height of the tower. Then \(x\) is (Acceleration due to gravity = 10 m/s\(^2\))
View Solution
The total height \(h = 125\) m and acceleration due to gravity \(g = 10\) m/s\(^2\).
Using the formula for the distance fallen in the last second \(h = \frac{1}{2}g(t-1)^2 - \frac{1}{2}gt^2\): \[ t = \sqrt{\frac{2h}{g}} = \sqrt{\frac{2 \times 125}{10}} = 5 seconds \]
Distance fallen in the last second: \[ h = \frac{1}{2}g(5-1)^2 - \frac{1}{2}g(5)^2 = 45 m \]
Thus, \(x = \frac{45}{125} \times 100 = 36%\). Quick Tip: Remember that the distance fallen in the last second can be found using the difference in distances from consecutive seconds.
A body P is projected at an angle of 30° with the horizontal and another body Q is projected at angle of 30° with the vertical. If the ratio of the horizontal ranges of the bodies P and Q is 1:2, then the ratio of the maximum heights reached by the bodies P and Q is
View Solution
To solve this problem, we need to analyze the projectile motions of bodies P and Q and determine the ratio of their maximum heights based on the given information about their horizontal ranges.
1. Projectile Motion Basics:
- The horizontal range \( R \) of a projectile launched with an initial velocity \( u \) at an angle \( \theta \) with the horizontal is given by:
\[ R = \frac{u^2 \sin(2\theta)}{g} \]
- The maximum height \( H \) reached by the projectile is:
\[ H = \frac{u^2 \sin^2(\theta)}{2g} \]
2. Given Information:
- Body P is projected at an angle of 30° with the horizontal.
- Body Q is projected at an angle of 30° with the vertical, which means it is projected at an angle of 60° with the horizontal.
- The ratio of the horizontal ranges of P and Q is 1:2.
3. Calculate the Ranges:
- For body P (\( \theta_P = 30° \)):
\[ R_P = \frac{u_P^2 \sin(60°)}{g} = \frac{u_P^2 \cdot \frac{\sqrt{3}}{2}}{g} \]
- For body Q (\( \theta_Q = 60° \)):
\[ R_Q = \frac{u_Q^2 \sin(120°)}{g} = \frac{u_Q^2 \cdot \frac{\sqrt{3}}{2}}{g} \]
- Given \( \frac{R_P}{R_Q} = \frac{1}{2} \):
\[ \frac{\frac{u_P^2 \cdot \frac{\sqrt{3}}{2}}{g}}{\frac{u_Q^2 \cdot \frac{\sqrt{3}}{2}}{g}} = \frac{1}{2} \implies \frac{u_P^2}{u_Q^2} = \frac{1}{2} \]
4. Calculate the Maximum Heights:
- For body P:
\[ H_P = \frac{u_P^2 \sin^2(30°)}{2g} = \frac{u_P^2 \cdot \left(\frac{1}{2}\right)^2}{2g} = \frac{u_P^2}{8g} \]
- For body Q:
\[ H_Q = \frac{u_Q^2 \sin^2(60°)}{2g} = \frac{u_Q^2 \cdot \left(\frac{\sqrt{3}}{2}\right)^2}{2g} = \frac{3u_Q^2}{8g} \]
- Using \( \frac{u_P^2}{u_Q^2} = \frac{1}{2} \):
\[ H_P = \frac{u_P^2}{8g} = \frac{1}{2} \cdot \frac{u_Q^2}{8g} = \frac{u_Q^2}{16g} \]
\[ H_Q = \frac{3u_Q^2}{8g} \]
- Therefore, the ratio \( \frac{H_P}{H_Q} \) is:
\[ \frac{H_P}{H_Q} = \frac{\frac{u_Q^2}{16g}}{\frac{3u_Q^2}{8g}} = \frac{1}{16} \cdot \frac{8}{3} = \frac{1}{6} \]
5. Final Answer:
- The ratio of the maximum heights reached by bodies P and Q is:
\[ \boxed{1:6} \]
This corresponds to option (2). Quick Tip: Use trigonometric identities and properties to analyze projectile motion, noting symmetry in angles.
A car is moving on a circular track banked at an angle of 45°. If the maximum permissible speed of the car to avoid slipping is twice the optimum speed of the car to avoid the wear and tear of the tyres, then the coefficient of static friction between the wheels of the car and the road is
View Solution
Let's analyze the situation.
Let the radius of the circular track be \(r\).
The angle of banking is \(\theta = 45^\circ\).
The maximum permissible speed to avoid slipping is \(v_{max}\).
The optimum speed to avoid wear and tear is \(v_{opt}\).
Given that \(v_{max} = 2 v_{opt}\).
The optimum speed \(v_{opt}\) is the speed at which no frictional force is required.
\(v_{opt} = \sqrt{rg \tan \theta}\)
Since \(\theta = 45^\circ\), \(\tan \theta = \tan 45^\circ = 1\).
\(v_{opt} = \sqrt{rg}\)
The maximum permissible speed to avoid slipping is given by:
\(v_{max} = \sqrt{rg \left( \frac{\tan \theta + \mu_s}{1 - \mu_s \tan \theta} \right)}\)
where \(\mu_s\) is the coefficient of static friction.
Given \(v_{max} = 2 v_{opt}\), we have:
\(2 \sqrt{rg} = \sqrt{rg \left( \frac{\tan \theta + \mu_s}{1 - \mu_s \tan \theta} \right)}\)
Squaring both sides, we get:
\(4 rg = rg \left( \frac{\tan \theta + \mu_s}{1 - \mu_s \tan \theta} \right)\)
\(4 = \frac{\tan \theta + \mu_s}{1 - \mu_s \tan \theta}\)
Since \(\theta = 45^\circ\), \(\tan \theta = 1\).
\(4 = \frac{1 + \mu_s}{1 - \mu_s}\)
\(4(1 - \mu_s) = 1 + \mu_s\)
\(4 - 4\mu_s = 1 + \mu_s\)
\(3 = 5 \mu_s\)
\(\mu_s = \frac{3}{5} = 0.6\)
Therefore, the coefficient of static friction between the wheels of the car and the road is 0.6.
Final Answer: The final answer is \(\boxed{(4)}\) Quick Tip: Remember that the relationship between maximum and optimum speeds on a banked curve involves both gravitational and frictional forces.
A block of mass 0.5 kg is at rest on a horizontal table. The coefficient of kinetic friction between the table and the block is 0.2. If a horizontal force of 5 N is applied on the block, the kinetic energy of the block in a time of 4 s is (Acceleration due to gravity = 10 m/s\(^2\))
View Solution
Let's solve the problem step-by-step.
Given:
Mass of the block, \(m = 0.5\) kg
Coefficient of kinetic friction, \(\mu_k = 0.2\)
Applied horizontal force, \(F = 5\) N
Time, \(t = 4\) s
Acceleration due to gravity, \(g = 10\) m/s\(^2\)
First, calculate the frictional force acting on the block: \(F_f = \mu_k \times N = \mu_k \times mg\) \(F_f = 0.2 \times 0.5 \times 10 = 1\) N
Next, calculate the net force acting on the block: \(F_{net} = F - F_f = 5 - 1 = 4\) N
Now, calculate the acceleration of the block: \(a = \frac{F_{net}}{m} = \frac{4}{0.5} = 8\) m/s\(^2\)
Calculate the final velocity of the block after 4 seconds: \(v = u + at\)
Since the block starts from rest, \(u = 0\). \(v = 0 + 8 \times 4 = 32\) m/s
Finally, calculate the kinetic energy of the block: \(KE = \frac{1}{2} m v^2 = \frac{1}{2} \times 0.5 \times (32)^2 = 0.25 \times 1024 = 256\) J
Therefore, the kinetic energy of the block after 4 seconds is 256 J.
Final Answer: The final answer is \(\boxed{(3)}\) Quick Tip: Apply Newton's second law to find acceleration and use kinetic energy formula to calculate energy.
The sphere A of mass \( m \) moving with a constant velocity hits another sphere B of mass \( 2m \) at rest. If the coefficient of restitution is 0.4, the ratio of the velocities of the spheres A and B after collision is
View Solution
Let's solve the problem step by step:
Let the mass of sphere A be \(m_A = m\) and its initial velocity be \(u_A = u\).
Let the mass of sphere B be \(m_B = 2m\) and its initial velocity be \(u_B = 0\).
The coefficient of restitution is \(e = 0.4\).
Let the final velocities of spheres A and B be \(v_A\) and \(v_B\), respectively.
We have two equations:
1. Conservation of momentum: \(m_A u_A + m_B u_B = m_A v_A + m_B v_B\)
2. Coefficient of restitution: \(e = \frac{v_B - v_A}{u_A - u_B}\)
Substituting the given values:
1. \(m(u) + 2m(0) = m v_A + 2m v_B\) \(mu = m v_A + 2m v_B\) \(u = v_A + 2v_B\) (1)
2. \(0.4 = \frac{v_B - v_A}{u - 0}\) \(0.4u = v_B - v_A\) (2)
From (1), we have \(v_A = u - 2v_B\).
Substituting this into (2): \(0.4u = v_B - (u - 2v_B)\) \(0.4u = v_B - u + 2v_B\) \(0.4u = 3v_B - u\) \(1.4u = 3v_B\) \(v_B = \frac{1.4u}{3} = \frac{14u}{30} = \frac{7u}{15}\)
Now, substitute \(v_B\) back into the equation for \(v_A\): \(v_A = u - 2v_B = u - 2(\frac{7u}{15}) = u - \frac{14u}{15} = \frac{15u - 14u}{15} = \frac{u}{15}\)
Now, find the ratio \(v_A : v_B\): \(\frac{v_A}{v_B} = \frac{\frac{u}{15}}{\frac{7u}{15}} = \frac{u}{15} \times \frac{15}{7u} = \frac{1}{7}\)
Therefore, the ratio of the velocities of the spheres A and B after the collision is 1:7.
Final Answer: The final answer is \(\boxed{(3)}\) Quick Tip: Use both the coefficient of restitution and conservation of momentum to solve for velocities after collision.
A solid sphere rolls down without slipping from the top of an inclined plane of height 28 m and angle of inclination 30°. The velocity of the sphere when it reaches the bottom of the plane is (Acceleration due to gravity \( g = 10 \, m/s^2 \))
View Solution
Let's solve the problem step by step.
Given:
Height of the inclined plane, \(h = 28\) m
Angle of inclination, \(\theta = 30^\circ\)
Acceleration due to gravity, \(g = 10\) m/s\(^2\)
The sphere rolls without slipping.
The velocity of a rolling solid sphere at the bottom of an inclined plane is given by: \(v = \sqrt{\frac{2gh}{1 + \frac{I}{mr^2}}}\)
where \(I\) is the moment of inertia of the solid sphere, \(m\) is its mass, and \(r\) is its radius.
For a solid sphere, the moment of inertia is \(I = \frac{2}{5} mr^2\).
So, \(\frac{I}{mr^2} = \frac{\frac{2}{5} mr^2}{mr^2} = \frac{2}{5}\).
Now, substitute the values into the velocity equation: \(v = \sqrt{\frac{2gh}{1 + \frac{2}{5}}} = \sqrt{\frac{2gh}{\frac{7}{5}}} = \sqrt{\frac{10gh}{7}}\)
Plug in the given values: \(v = \sqrt{\frac{10 \times 10 \times 28}{7}} = \sqrt{\frac{2800}{7}} = \sqrt{400} = 20\) m/s
Therefore, the velocity of the sphere when it reaches the bottom of the plane is 20 m/s.
Final Answer: The final answer is \(\boxed{(1)}\) Quick Tip: For rolling motion, use energy conservation considering both translational and rotational kinetic energy.
Four identical particles each of mass 'm' are kept at the four corners of a square of side 'a'. If one of the particles is removed, the shift in the position of the centre of mass is:
View Solution
Let the vertices of the square be A(0,0), B(a,0), C(a,a), D(0,a).
The coordinates of the center of mass when all four particles are present is: \(\)x_{cm = \frac{m(0) + m(a) + m(a) + m(0){4m = \frac{2ma{4m = \frac{a{2\(\) \(\)y_{cm = \frac{m(0) + m(0) + m(a) + m(a){4m = \frac{2ma{4m = \frac{a{2\(\)
The center of mass is \((\frac{a}{2}, \frac{a}{2})\).
Now, let's remove the particle at A(0,0). The new coordinates of the center of mass are: \(\)x_{cm' = \frac{m(a) + m(a) + m(0){3m = \frac{2ma{3m = \frac{2a{3\(\) \(\)y_{cm' = \frac{m(0) + m(a) + m(a){3m = \frac{2ma{3m = \frac{2a{3\(\)
The new center of mass is \((\frac{2a}{3}, \frac{2a}{3})\).
The shift in the position of the center of mass is the distance between the two points: \(\)d = \sqrt{\left(\frac{2a{3 - \frac{a{2\right)^2 + \left(\frac{2a{3 - \frac{a{2\right)^2\(\) \(\)d = \sqrt{2\left(\frac{4a-3a{6\right)^2 = \sqrt{2\left(\frac{a{6\right)^2 = \sqrt{2 \cdot \frac{a{6 = \frac{a\sqrt{2{6 = \frac{a{3\sqrt{2\(\) Quick Tip: The center of mass of a system of particles is the average position of the particles, weighted by their masses.
In a time ‘t", the amplitude of vibrations of a damped oscillator becomes half of its initial value, then the mechanical energy of the oscillator decreases by:
View Solution
The mechanical energy of a damped oscillator is proportional to the square of its amplitude: \[ E \propto A^2 \]
Given that the amplitude becomes half of its initial value: \[ A' = \frac{A}{2} \]
The new mechanical energy is: \[ E' = k \left(\frac{A}{2}\right)^2 = \frac{1}{4} kA^2 \]
The percentage decrease in energy is: \[ \frac{E - E'}{E} \times 100 = \frac{kA^2 - \frac{1}{4}kA^2}{kA^2} \times 100 \]
\[ = \left(1 - \frac{1}{4}\right) \times 100 = 75% \] Quick Tip: The energy of a damped oscillator decreases exponentially over time, and when the amplitude is halved, the energy reduces to one-fourth of its initial value.
The energy required to take a body from the surface of the earth to a height equal to the radius of the earth is \( W \). The energy required to take this body from the surface of the earth to a height equal to twice the radius of the earth is:
View Solution
The energy required to move a body from the surface of the Earth to a height \( h \) is given by:
\[ W = GMm \left(\frac{1}{R} - \frac{1}{R+h}\right) \]
For height \( h = R \):
\[ W_1 = GMm \left(\frac{1}{R} - \frac{1}{2R}\right) = \frac{GMm}{2R} = W \]
For height \( h = 2R \):
\[ W_2 = GMm \left(\frac{1}{R} - \frac{1}{3R}\right) = \frac{2GMm}{3R} = \frac{4W}{3} \]
Thus, the required energy is \( \frac{4W}{3} \). Quick Tip: The gravitational potential energy change follows an inverse relationship with distance, making energy calculations crucial in celestial mechanics.
A steel wire of length 3 m and a copper wire of length 2.2 m are connected end to end. When the combination is stretched by a force, the net elongation is 1.05 mm. If the area of cross-section of each wire is 6 mm², then the load applied is:
(Young’s moduli of steel and copper are respectively \(2 \times 10^{11} \, Nm^{-2}\) and \(1.1 \times 10^{11} \, Nm^{-2}\)).
View Solution
To determine the load applied to the combination of steel and copper wires, we need to use the concept of Young's modulus, which relates stress and strain in a material.
1. Given Data:
- Length of steel wire, \( L_s = 3 \, m \)
- Length of copper wire, \( L_c = 2.2 \, m \)
- Total elongation, \( \Delta L = 1.05 \, mm = 1.05 \times 10^{-3} \, m \)
- Cross-sectional area of each wire, \( A = 6 \, mm^2 = 6 \times 10^{-6} \, m^2 \)
- Young’s modulus of steel, \( Y_s = 2 \times 10^{11} \, Nm^{-2} \)
- Young’s modulus of copper, \( Y_c = 1.1 \times 10^{11} \, Nm^{-2} \)
2. Calculate the Elongation for Each Wire:
- The total elongation is the sum of the elongations of the steel and copper wires:
\[ \Delta L = \Delta L_s + \Delta L_c \]
- Using Young's modulus formula \( \Delta L = \frac{F L}{A Y} \), we can express the elongations as:
\[ \Delta L_s = \frac{F L_s}{A Y_s} \]
\[ \Delta L_c = \frac{F L_c}{A Y_c} \]
- Therefore:
\[ \Delta L = \frac{F L_s}{A Y_s} + \frac{F L_c}{A Y_c} \]
\[ 1.05 \times 10^{-3} = F \left( \frac{L_s}{A Y_s} + \frac{L_c}{A Y_c} \right) \]
3. Substitute the Given Values:
\[ 1.05 \times 10^{-3} = F \left( \frac{3}{6 \times 10^{-6} \times 2 \times 10^{11}} + \frac{2.2}{6 \times 10^{-6} \times 1.1 \times 10^{11}} \right) \]
\[ 1.05 \times 10^{-3} = F \left( \frac{3}{1.2 \times 10^{6}} + \frac{2.2}{6.6 \times 10^{5}} \right) \]
\[ 1.05 \times 10^{-3} = F \left( 2.5 \times 10^{-6} + 3.333 \times 10^{-6} \right) \]
\[ 1.05 \times 10^{-3} = F \left( 5.833 \times 10^{-6} \right) \]
4. Solve for the Force \( F \):
\[ F = \frac{1.05 \times 10^{-3}}{5.833 \times 10^{-6}} \approx 180 \, N \]
5. Final Answer:
- The load applied is:
\[ \boxed{180 \, N} \]
This corresponds to option (1). Quick Tip: The total elongation in a series combination of wires is the sum of the elongations of individual wires under the same force.
The height of water level in a tank of uniform cross-section is 5 m. The volume of the water leaked in 5 s through a hole of area \(2.4~mm^{2}\) made at the bottom of the tank is (Assume the level of the water in the tank remains constant and acceleration due to gravity \(=10~ms^{-2}\))
View Solution
The velocity of water coming out of the hole is given by Torricelli's theorem: \[ v = \sqrt{2gh} \]
where \( g \) is the acceleration due to gravity and \( h \) is the height of the water level.
Given:
\( h = 5 \) m
\( g = 10 \) ms\(^{-2}\)
Therefore, \[ v = \sqrt{2 \times 10 \times 5} = \sqrt{100} = 10 m/s \]
The area of the hole is given as \( A = 2.4 mm^2 = 2.4 \times 10^{-6} m^2 \).
The volume flow rate \( Q \) is given by: \[ Q = Av \] \[ Q = 2.4 \times 10^{-6} m^2 \times 10 m/s = 2.4 \times 10^{-5} m^3/s \]
The volume of water leaked in 5 seconds is: \[ V = Q \times t \] \[ V = 2.4 \times 10^{-5} m^3/s \times 5 s = 12 \times 10^{-5} m^3 = 120 \times 10^{-6} m^3 \]
Therefore, the volume of water leaked in 5 seconds is \( 120 \times 10^{-6} m^3 \). Quick Tip: Torricelli's theorem is a special case of Bernoulli's principle. It states that the speed of efflux of a fluid through a sharp-edged orifice at the bottom of a tank filled to a depth \(h\) is the same as the speed that a body would acquire in falling freely from a height \(h\).
The work done in increasing the diameter of a soap bubble from 2 cm to 4 cm is (Surface tension of soap solution \(=3.5\times10^{-2}Nm^{-1}\))
View Solution
The work done in increasing the surface area of a soap bubble is given by: \[ W = T \Delta A \]
where \( T \) is the surface tension and \( \Delta A \) is the change in surface area.
The surface area of a soap bubble is given by \( A = 2 \times 4\pi r^2 \) since it has two surfaces.
Given:
Initial diameter \( d_1 = 2 \) cm, so initial radius \( r_1 = 1 \) cm \(= 0.01 \) m
Final diameter \( d_2 = 4 \) cm, so final radius \( r_2 = 2 \) cm \(= 0.02 \) m
Surface tension \( T = 3.5 \times 10^{-2} \) Nm\(^{-1}\)
Initial surface area: \[ A_1 = 2 \times 4\pi r_1^2 = 8\pi (0.01)^2 = 8\pi \times 10^{-4} m^2 \]
Final surface area: \[ A_2 = 2 \times 4\pi r_2^2 = 8\pi (0.02)^2 = 8\pi \times 4 \times 10^{-4} = 32\pi \times 10^{-4} m^2 \]
Change in surface area: \[ \Delta A = A_2 - A_1 = 32\pi \times 10^{-4} - 8\pi \times 10^{-4} = 24\pi \times 10^{-4} m^2 \]
Work done: \[ W = T \Delta A = 3.5 \times 10^{-2} \times 24\pi \times 10^{-4} \] \[ W = 84\pi \times 10^{-6} \] \[ W \approx 84 \times 3.14 \times 10^{-6} \] \[ W \approx 263.76 \times 10^{-6} J \]
This is approximately \( 264 \times 10^{-6} \) J.
Final Answer: (2) \(264\times10^{-6}\) J Quick Tip: Remember that a soap bubble has two surfaces (inner and outer), so the surface area is twice the area of a sphere.
The temperature on a Fahrenheit temperature scale that is twice the temperature on a Celsius temperature scale is:
View Solution
We use the Fahrenheit-Celsius conversion formula:
\[ F = \frac{9}{5}C + 32 \]
Given that the Fahrenheit temperature is twice the Celsius temperature:
\[ F = 2C \]
Substituting \( F = \frac{9}{5}C + 32 \):
\[ 2C = \frac{9}{5}C + 32 \]
Solving for \( C \):
\[ 2C - \frac{9}{5}C = 32 \]
\[ \frac{10C - 9C}{5} = 32 \]
\[ \frac{C}{5} = 32 \]
\[ C = 160^\circ C \]
\[ F = 2C = 320^\circ F \] Quick Tip: The relation \( F = \frac{9}{5}C + 32 \) helps in converting temperatures between Celsius and Fahrenheit.
The temperatures of equal masses of three different liquids A, B, and C are \(15^\circ C\), \(24^\circ C\), and \(30^\circ C\) respectively. The resultant temperature when liquids A and B are mixed is \(20^\circ C\) and when liquids B and C are mixed is \(26^\circ C\). Then the ratio of specific heat capacities of the liquids A, B, and C is:
View Solution
Using the principle of calorimetry:
\[ m_A c_A (T_f - T_A) = m_B c_B (T_B - T_f) \]
\[ c_A (20 - 15) = c_B (24 - 20) \]
\[ 5c_A = 4c_B \]
\[ c_A = \frac{4}{5}c_B \]
For B and C:
\[ c_B (26 - 24) = c_C (30 - 26) \]
\[ 2c_B = 4c_C \]
\[ c_C = \frac{1}{2} c_B \]
Thus, the ratio is:
\[ c_A : c_B : c_C = \frac{4}{5} : 1 : \frac{1}{2} \]
\[ 8:10:5 \] Quick Tip: The principle of calorimetry states that heat lost = heat gained when two substances mix.
The efficiency of a reversible heat engine working between two temperatures is 50%. The coefficient of performance of a refrigerator working between the same two temperatures but in reverse direction is:
View Solution
The efficiency of a heat engine is:
\[ \eta = \frac{T_H - T_C}{T_H} = 0.5 \]
\[ \frac{T_H - T_C}{T_H} = \frac{1}{2} \]
\[ T_H - T_C = \frac{T_H}{2} \]
\[ T_H = 2T_C \]
The coefficient of performance (COP) of a refrigerator is given by:
\[ COP = \frac{T_C}{T_H - T_C} \]
\[ COP = \frac{T_C}{T_H - T_C} = \frac{T_C}{T_C} = 1 \] Quick Tip: COP of a refrigerator is the inverse of the efficiency difference of a heat engine operating between the same temperatures.
The total internal energy of 4 moles of a diatomic gas at a temperature of \(27^\circ C\) is:
(Universal gas constant \( R = 8.31 \, J mol^{-1} K^{-1} \))
View Solution
The internal energy of a diatomic gas is given by:
\[ U = \frac{5}{2} n R T \]
where:
- \( n = 4 \) (number of moles),
- \( R = 8.31 \, J mol^{-1} K^{-1} \) (universal gas constant),
- \( T = 27 + 273 = 300 \) K (temperature in Kelvin).
\[ U = \frac{5}{2} \times 4 \times 8.31 \times 300 \]
\[ U = 24.93 \, kJ \] Quick Tip: For diatomic gases, the internal energy is calculated using \( U = \frac{5}{2} n R T \) because of the degrees of freedom.
A car travelling at a speed of \(54 \, kmph\) towards a wall sounds a horn of frequency \(400 \, Hz\). The difference in the frequencies of two sounds, one received directly from the car and the other reflected from the wall, noticed by a person standing between the car and the wall is:
(Speed of sound in air is \(335 \, m/s\))
View Solution
To solve this problem, we need to calculate the difference in frequencies between the sound received directly from the car and the sound reflected from the wall. This involves the Doppler effect for both the approaching car and the reflected sound.
1. Convert the car's speed to meters per second:
\[ 54 \, kmph = 54 \times \frac{1000}{3600} = 15 \, m/s \]
2. Calculate the frequency received directly from the car:
- The observer is stationary, and the car is moving towards the observer.
- The formula for the Doppler effect when the source is moving towards the observer is:
\[ f_{direct} = \frac{v}{v - v_s} f_0 \]
where \( v = 335 \, m/s \) (speed of sound), \( v_s = 15 \, m/s \) (speed of the car), and \( f_0 = 400 \, Hz \) (original frequency).
- Plugging in the values:
\[ f_{direct} = \frac{335}{335 - 15} \times 400 = \frac{335}{320} \times 400 \approx 418.75 \, Hz \]
3. Calculate the frequency of the sound reflected from the wall:
- The car is moving towards the wall, so the frequency of the sound hitting the wall is:
\[ f_{wall} = \frac{v}{v - v_s} f_0 = \frac{335}{320} \times 400 \approx 418.75 \, Hz \]
- The wall reflects this frequency, and the observer hears the reflected sound. Since the wall is stationary, the frequency received by the observer from the wall is the same as the frequency hitting the wall:
\[ f_{reflected} = 418.75 \, Hz \]
4. Calculate the difference in frequencies:
- The difference between the directly received frequency and the reflected frequency is:
\[ \Delta f = f_{reflected} - f_{direct} = 418.75 - 418.75 = 0 \, Hz \]
5. Final Answer:
- The difference in the frequencies noticed by the person is:
\[ \boxed{0} \]
This corresponds to option (4). Quick Tip: The Doppler effect occurs due to relative motion between the sound source and the observer, affecting the perceived frequency.
The speed of a transverse wave in a stretched string 'A' is 'v'. Another string 'B' of same length and same radius is subjected to same tension. If the density of the material of the string 'B' is 2% more than that of 'A', then the speed of the transverse wave in string 'B' is
View Solution
The speed of a transverse wave in a stretched string is given by: \(\)v = \sqrt{\frac{T{\mu\(\)
where \(T\) is the tension and \(\mu\) is the linear mass density.
The linear mass density is given by: \(\)\mu = \frac{m{L = \frac{\rho V{L = \frac{\rho A L{L = \rho A\(\)
where \(\rho\) is the density of the material and \(A\) is the cross-sectional area.
Since the length and radius of the strings are the same, the cross-sectional area is the same.
Let \(\rho_A\) and \(\rho_B\) be the densities of strings A and B respectively.
We are given that \(\rho_B = \rho_A + 0.02\rho_A = 1.02\rho_A\).
Let \(v_A\) and \(v_B\) be the speeds of the transverse waves in strings A and B respectively.
We have: \(\)v_A = \sqrt{\frac{T{\rho_A A = v\(\) \(\)v_B = \sqrt{\frac{T{\rho_B A = \sqrt{\frac{T{1.02\rho_A A\(\)
We can write: \(\)\frac{v_B{v_A = \sqrt{\frac{\rho_A A{1.02\rho_A A = \sqrt{\frac{1{1.02\(\) \(\)v_B = v_A \sqrt{\frac{1{1.02 = \frac{v{\sqrt{1.02\(\) Quick Tip: The speed of a transverse wave in a string is inversely proportional to the square root of the linear mass density.
For a combination of two convex lenses of focal lengths \( f_1 \) and \( f_2 \) to act as a glass slab, the distance of separation between them is:
View Solution
For two convex lenses to act as a glass slab, the net optical path difference should be zero. This happens when the separation between the lenses is equal to the sum of their focal lengths:
\[ d = f_1 + f_2 \] Quick Tip: When two convex lenses act as a glass slab, the optical path remains unchanged, requiring a separation of \( f_1 + f_2 \).
If a ray of light passes through an equilateral prism such that the angle of incidence and the angle of emergence are both equal to 70% of the angle of the prism, then the angle of minimum deviation is:
View Solution
For an equilateral prism with angle \( A \), when the angle of incidence and emergence are equal, the condition for minimum deviation holds:
\[ D_m = 2i - A \]
Given \( i = 0.7A \):
\[ D_m = 2(0.7A) - A = 1.4A - A = 0.4A \]
For an equilateral prism, \( A = 60^\circ \):
\[ D_m = 0.4 \times 60 = 24^\circ \] Quick Tip: At minimum deviation, the angle of incidence and emergence are equal, simplifying calculations for the deviation angle.
Young’s double slit experiment is performed with monochromatic light of wavelength \( 6000 Å \). If the intensity of light at a point on the screen where path difference is \( 2000 Å \) is \( I_1 \) and the intensity of light at a point where path difference is \( 1000 Å \) is \( I_2 \), then the ratio \( I_1 : I_2 \) is:
View Solution
To determine the ratio \( I_1 : I_2 \) in Young’s double slit experiment, we need to analyze the interference pattern and how the path difference affects the intensity of light at different points on the screen.
1. Given Data:
- Wavelength of light, \( \lambda = 6000 Å \)
- Path difference at point 1, \( \Delta_1 = 2000 Å \)
- Path difference at point 2, \( \Delta_2 = 1000 Å \)
- Intensity at point 1, \( I_1 \)
- Intensity at point 2, \( I_2 \)
2. Calculate the Phase Difference:
- The phase difference \( \phi \) is related to the path difference \( \Delta \) by:
\[ \phi = \frac{2\pi \Delta}{\lambda} \]
- For point 1:
\[ \phi_1 = \frac{2\pi \times 2000 Å}{6000 Å} = \frac{2\pi}{3} \]
- For point 2:
\[ \phi_2 = \frac{2\pi \times 1000 Å}{6000 Å} = \frac{\pi}{3} \]
3. Calculate the Intensity:
- The intensity \( I \) at a point on the screen is given by:
\[ I = 4I_0 \cos^2\left(\frac{\phi}{2}\right) \]
where \( I_0 \) is the intensity of light from a single slit.
- For point 1:
\[ I_1 = 4I_0 \cos^2\left(\frac{\phi_1}{2}\right) = 4I_0 \cos^2\left(\frac{\pi}{3}\right) = 4I_0 \left(\frac{1}{2}\right)^2 = I_0 \]
- For point 2:
\[ I_2 = 4I_0 \cos^2\left(\frac{\phi_2}{2}\right) = 4I_0 \cos^2\left(\frac{\pi}{6}\right) = 4I_0 \left(\frac{\sqrt{3}}{2}\right)^2 = 3I_0 \]
4. Determine the Ratio \( I_1 : I_2 \):
- The ratio of the intensities is:
\[ I_1 : I_2 = I_0 : 3I_0 = 1 : 3 \]
5. Final Answer:
- The ratio \( I_1 : I_2 \) is:
\[ \boxed{1:3} \]
This corresponds to option (1). Quick Tip: In YDSE, intensity variation depends on the cosine square of the phase difference, affecting the bright and dark fringes.
Two positive point charges are separated by a distance of 4 m in air. If the sum of the two charges is \( 36 \mu C \) and the electrostatic force between them is \( 0.18 \) N, then the bigger charge is:
View Solution
Using Coulomb’s law:
\[ F = k \frac{q_1 q_2}{r^2} \]
where:
- \( k = 9 \times 10^9 \, Nm^2C^{-2} \),
- \( r = 4 \) m,
- \( q_1 + q_2 = 36 \mu C \),
- \( F = 0.18 \) N.
Substituting values:
\[ 0.18 = 9 \times 10^9 \times \frac{q_1 q_2}{4^2} \]
\[ q_1 q_2 = \frac{0.18 \times 16}{9 \times 10^9} \times 10^{-12} \]
\[ q_1 q_2 = 3.2 \times 10^{-12} C^2 \]
Solving for \( q_1, q_2 \):
\[ q_1, q_2 = \frac{36 \pm \sqrt{36^2 - 4 \times 3.2}}{2} \]
\[ q_1 = 20 \mu C, \quad q_2 = 16 \mu C \]
Thus, the larger charge is \( 20 \mu C \). Quick Tip: In Coulomb’s law problems, solving quadratic equations often helps determine individual charges when their sum is given.
Three capacitors of capacitances 10 \(\mu\)F, 5 \(\mu\)F and 20 \(\mu\)F are connected in series with a 14 V dc supply. The charge on 5 \(\mu\)F capacitor is
View Solution
When capacitors are connected in series, the charge on each capacitor is the same. The equivalent capacitance of the series combination is \[\frac{1}{C} = \frac{1}{10} + \frac{1}{5} + \frac{1}{20} = \frac{2 + 4 + 1}{20} = \frac{7}{20},\]so \(C = \frac{20}{7} \, \mu\)F. The charge on this equivalent capacitor is \[ Q = CV = \frac{20}{7} \times 14 = 40 \, \mu C. \]
This is also the charge on the \( 5 \, \mu F \) capacitor. Quick Tip: When capacitors are connected in series, the reciprocal of the equivalent capacitance is the sum of the reciprocals of the individual capacitances.
When the temperature of a wire is increased from 303 K to 356 K, the resistance of the wire increases by 10%. The temperature coefficient of resistance of the material of the wire is:
View Solution
The resistance-temperature relation is given by:
\[ R_T = R_0 (1 + \alpha \Delta T) \]
where:
- \( R_T = 1.1 R_0 \) (given increase by 10%),
- \( \Delta T = 356 - 303 = 53 K \),
- \( \alpha \) is the temperature coefficient.
\[ 1.1 R_0 = R_0 (1 + \alpha \times 53) \]
\[ 1.1 = 1 + 53\alpha \]
\[ \alpha = \frac{0.1}{53} = 1.88 \times 10^{-3} \approx 2 \times 10^{-3} \] Quick Tip: The temperature coefficient of resistance is calculated from the fractional change in resistance per unit temperature change.
Three resistors of resistances \(10 \Omega\), \(20 \Omega\), and \(30 \Omega\) are connected as shown in the figure. If the points A, B, and C are at potentials \(10 V\), \(6 V\), and \(5 V\) respectively, then the ratio of the magnitudes of the currents through \(10 \Omega\) and \(30 \Omega\) resistors is:
View Solution
Using Ohm's Law \( I = \frac{V}{R} \),
For the \( 10 \Omega \) resistor:
\[ I_1 = \frac{V_A - V_B}{10} = \frac{10 - 6}{10} = \frac{4}{10} = 0.4 A \]
For the \( 30 \Omega \) resistor:
\[ I_2 = \frac{V_B - V_C}{30} = \frac{6 - 5}{30} = \frac{1}{30} = 0.2 A \]
Ratio:
\[ I_1 : I_2 = 0.4 : 0.2 = 2:1 \] Quick Tip: In a parallel circuit, currents through different branches depend on both the resistance and the potential difference across them.
A particle of charge \( 2 C \) is moving with a velocity \( (3\hat{i} + 4\hat{j}) \) m/s in the presence of magnetic and electric fields. If the magnetic field is \( ( \hat{i} + 2\hat{j} + 3\hat{k} ) \) T and the electric field is \( (-2\hat{k}) \) NC\(^{-1}\), then the Lorentz force on the particle is:
View Solution
The Lorentz force is given by:
\[ \vec{F} = q (\vec{E} + \vec{v} \times \vec{B}) \]
First, calculate the cross product \( \vec{v} \times \vec{B} \):
\[ \begin{vmatrix} \hat{i} & \hat{j} & \hat{k}
3 & 4 & 0
1 & 2 & 3 \end{vmatrix} \]
\[ = \hat{i} (4 \times 3 - 0 \times 2) - \hat{j} (3 \times 3 - 0 \times 1) + \hat{k} (3 \times 2 - 4 \times 1) \]
\[ = \hat{i} (12) - \hat{j} (9) + \hat{k} (6 - 4) \]
\[ = 12\hat{i} - 9\hat{j} + 2\hat{k} \]
Now, adding \( \vec{E} \):
\[ \vec{E} + \vec{v} \times \vec{B} = (12\hat{i} - 9\hat{j} + 2\hat{k}) + (-2\hat{k}) \]
\[ = 12\hat{i} - 9\hat{j} + 0\hat{k} \]
Multiplying by \( q = 2 C \):
\[ \vec{F} = 2 (12\hat{i} - 9\hat{j} + 0\hat{k}) = 24\hat{i} - 18\hat{j} \]
Magnitude:
\[ |\vec{F}| = \sqrt{(24)^2 + (-18)^2} \]
\[ = \sqrt{576 + 324} = \sqrt{900} = 30 N \] Quick Tip: Lorentz force accounts for both electric and magnetic effects on a charged particle, calculated as \( q(\vec{E} + \vec{v} \times \vec{B}) \).
A rectangular coil of 400 turns and \(10^{-2} \, m^2\) area, carrying a current of 0.5 A is placed in a uniform magnetic field of 1 T such that the plane of the coil makes an angle of 60° with the direction of the magnetic field. The initial moment of force acting on the coil in Nm is:
View Solution
We are tasked with finding the initial moment of force (torque) acting on a rectangular coil placed in a uniform magnetic field. The given parameters are:
Number of turns, \(N = 400\),
Area of the coil, \(A = 10^{-2} \, m^2\),
Current through the coil, \(I = 0.5 \, A\),
Magnetic field strength, \(B = 1 \, T\),
Angle between the plane of the coil and the magnetic field, \(\theta = 60^\circ\).
Step 1: Recall the formula for torque on a current-carrying coil
The torque (\(\tau\)) acting on a current-carrying coil in a magnetic field is given by:
\[ \tau = N \cdot I \cdot A \cdot B \cdot \sin(\phi) \]
where:
\(N\) is the number of turns,
\(I\) is the current,
\(A\) is the area of the coil,
\(B\) is the magnetic field strength,
\(\phi\) is the angle between the magnetic field and the normal to the plane of the coil.
Step 2: Determine the angle \(\phi\)
The angle \(\theta = 60^\circ\) is the angle between the plane of the coil and the magnetic field. The angle \(\phi\) is the angle between the normal to the plane of the coil and the magnetic field. These two angles are complementary, so:
\[ \phi = 90^\circ - \theta = 90^\circ - 60^\circ = 30^\circ \]
Step 3: Substitute values into the torque formula
Substitute the given values into the torque formula:
\[ \tau = N \cdot I \cdot A \cdot B \cdot \sin(\phi) \]
\[ \tau = 400 \cdot 0.5 \cdot 10^{-2} \cdot 1 \cdot \sin(30^\circ) \]
Simplify:
\[ \tau = 400 \cdot 0.5 \cdot 10^{-2} \cdot 1 \cdot 0.5 \]
\[ \tau = 400 \cdot 0.5 \cdot 10^{-2} \cdot 0.5 \]
\[ \tau = 400 \cdot 0.0025 \]
\[ \tau = 1 \, Nm \]
Thus, the initial moment of force acting on the coil is 1 Nm. Quick Tip: The torque on a coil in a magnetic field is maximum when the plane of the coil is perpendicular to the magnetic field and minimum when the plane is parallel to the field.
The most exotic diamagnetic materials are:
View Solution
Diamagnetic materials are those which are repelled by a magnetic field. Superconductors exhibit perfect diamagnetism, meaning they expel all magnetic fields when cooled below a certain temperature, which is why they are considered one of the most exotic diamagnetic materials. Quick Tip: Superconductors are unique in that they show perfect diamagnetism, a phenomenon known as the Meissner effect, which is absent in other materials like semiconductors or conductors.
Two circular coils of radii \(r_1\) and \(r_2\) (\(r_1 \ll r_2\)) are placed coaxially with their centers coinciding. The mutual inductance of the arrangement is:
View Solution
The mutual inductance \( M \) between two circular coils is given by:
\[ M = \frac{\mu_0 \pi r_1^2}{2 r_2} \]
where \( r_1 \) and \( r_2 \) are the radii of the coils, and \( r_1 \ll r_2 \) implies that the first coil is much smaller than the second coil. Quick Tip: In the case of coaxially placed circular coils with \( r_1 \ll r_2 \), the mutual inductance can be approximated using the formula \( \frac{\mu_0 \pi r_1^2}{2 r_2} \).
In a series LCR circuit, if the current leads the source voltage, then:
View Solution
In an LCR circuit, the phase relationship between voltage and current depends on the reactances:
\[ X_L = \omega L, \quad X_C = \frac{1}{\omega C} \]
The phase angle \( \phi \) is given by:
\[ \tan \phi = \frac{X_L - X_C}{R} \]
If the current leads the voltage, the circuit behaves like a capacitive circuit, meaning:
\[ X_C > X_L \] Quick Tip: In a series LCR circuit, the circuit is capacitive when \( X_C > X_L \), causing the current to lead the voltage.
If the amplitude of the magnetic field part of a harmonic electromagnetic wave in vacuum is \( 270 \) nT, the amplitude of the electric field part of the wave is:
View Solution
The relation between electric field amplitude \( E_0 \) and magnetic field amplitude \( B_0 \) in an electromagnetic wave is:
\[ E_0 = c B_0 \]
where \( c = 3 \times 10^8 \) m/s and \( B_0 = 270 \times 10^{-9} \) T.
\[ E_0 = (3 \times 10^8) \times (270 \times 10^{-9}) \]
\[ E_0 = 81 \, NC^{-1} \] Quick Tip: The amplitudes of electric and magnetic fields in an EM wave are related by \( E_0 = c B_0 \).
If Planck’s constant is \( 6.63 \times 10^{-34} \) Js, then the slope of a graph drawn between cut-off voltage and frequency of incident light in a photoelectric experiment is:
View Solution
The equation for the photoelectric effect is:
\[ eV_s = h f - \phi \]
where:
- \( e \) is the elementary charge (\( 1.6 \times 10^{-19} \) C),
- \( V_s \) is the stopping potential,
- \( h \) is Planck’s constant (\( 6.63 \times 10^{-34} \) Js),
- \( f \) is the frequency of incident light.
The slope of the \( V_s \) vs \( f \) graph is:
\[ \frac{h}{e} = \frac{6.63 \times 10^{-34}}{1.6 \times 10^{-19}} \]
\[ = 4.14 \times 10^{-15} Vs \] Quick Tip: The slope of the stopping potential vs frequency graph in a photoelectric experiment gives \( h/e \).
At room temperature, gaseous hydrogen is bombarded with a beam of electrons of 13.6 eV energy. The series to which the emitted spectral line belongs to:
View Solution
The energy of 13.6 eV corresponds to the ionization energy of hydrogen, meaning the electron is excited to the highest possible energy level and then de-excites.
The emitted spectral lines belong to the Lyman series when an electron transitions to the \( n=1 \) energy level:
\[ \Delta E = h \nu = 13.6 \left( 1 - \frac{1}{n^2} \right) eV \]
Since all transitions end at \( n=1 \), the emitted radiation falls in the ultraviolet region, characteristic of the Lyman series. Quick Tip: The Lyman series corresponds to electronic transitions where the final state is \( n = 1 \), producing ultraviolet radiation.
The half-life of a radioactive substance is 12 minutes. The time gap between 28% decay and 82% decay of the radioactive substance is:
View Solution
Radioactive decay follows the formula:
\[ N = N_0 e^{-\lambda t} \]
where the decay constant is related to half-life:
\[ \lambda = \frac{\ln 2}{T_{1/2}} \]
Given \( T_{1/2} = 12 \) min, the fraction remaining at 28% decay is:
\[ \frac{N}{N_0} = 0.72 \]
At 82% decay:
\[ \frac{N}{N_0} = 0.18 \]
Solving for \( t \):
\[ t = \frac{\ln(0.72)}{\ln(0.5)} \times 12 \]
\[ t = \frac{\ln(0.18)}{\ln(0.5)} \times 12 \]
The difference between the two times is 24 minutes. Quick Tip: The time gap between two decay levels is determined using the exponential decay formula.
An element consists of a mixture of three isotopes A, B, and C of masses \( m_1 \), \( m_2 \), and \( m_3 \) respectively. If the relative abundances of the three isotopes A, B, and C is in the ratio 2:3:5, the average mass of the element is:
View Solution
The average atomic mass is given by:
\[ M = \frac{2m_1 + 3m_2 + 5m_3}{2+3+5} \]
\[ = \frac{2m_1 + 3m_2 + 5m_3}{10} \]
\[ = 0.2m_1 + 0.3m_2 + 0.5m_3 \] Quick Tip: The average atomic mass is found using the weighted sum of isotopic masses divided by the total abundance.
The concentration of electrons in an intrinsic semiconductor is \( 6 \times 10^{15} \, m^{-3} \). On doping with an impurity, the electron concentration increases to \( 4 \times 10^{22} \, m^{-3} \). In thermal equilibrium, the concentration of the holes in the doped semiconductor is:
View Solution
For semiconductors, the intrinsic carrier concentration satisfies:
\[ n_i^2 = n_e n_h \]
where:
- \( n_i = 6 \times 10^{15} \, m^{-3} \),
- \( n_e = 4 \times 10^{22} \, m^{-3} \).
Solving for \( n_h \):
\[ n_h = \frac{n_i^2}{n_e} \]
\[ = \frac{(6 \times 10^{15})^2}{4 \times 10^{22}} \]
\[ = \frac{36 \times 10^{30}}{4 \times 10^{22}} \]
\[ = 9 \times 10^8 \, m^{-3} \] Quick Tip: In semiconductors, doping increases the electron concentration, reducing the hole concentration while maintaining \( n_i^2 = n_e n_h \).
Three logic gates are connected as shown in the figure. If the inputs are \( A = 1 \) and \( B = 1 \), then the values of \( y_1 \) and \( y_2 \) respectively are:
View Solution
For the given combination of logic gates:
First gate performs an AND operation, and since both inputs are \( A = 1 \) and \( B = 1 \), the output of the first gate (\( y_1 \)) will be \( 1 \).
The second gate performs a NAND operation, and since the input is \( A = 1 \) and \( B = 1 \), the output of the second gate (\( y_2 \)) will be \( 0 \).
Thus, the values of \( y_1 \) and \( y_2 \) are \( 0, 1 \), respectively. Quick Tip: For logic gates, remember that: - The AND gate outputs 1 if both inputs are 1, else it outputs 0. - The NAND gate outputs 0 if both inputs are 1, else it outputs 1.
The heights of the transmitting and receiving antennas are 33.8 m and 64.8 m respectively. The maximum distance between the antennas for satisfactory communication in line of sight mode is:
(Radius of the earth = 6400 km)
View Solution
To determine the maximum distance between the transmitting and receiving antennas for satisfactory communication in line of sight mode, we can use the formula for the line of sight distance between two antennas:
\[ d = \sqrt{2R h_t} + \sqrt{2R h_r} \]
where:
\( d \) is the maximum distance between the antennas,
\( R \) is the radius of the Earth,
\( h_t \) is the height of the transmitting antenna,
\( h_r \) is the height of the receiving antenna.
Given Data:
Height of transmitting antenna, \( h_t = 33.8 \, m \)
Height of receiving antenna, \( h_r = 64.8 \, m \)
Radius of the Earth, \( R = 6400 \, km = 6400 \times 10^3 \, m \)
Calculation:
1. Calculate the distance contributed by the transmitting antenna:
\[ d_t = \sqrt{2R h_t} = \sqrt{2 \times 6400 \times 10^3 \times 33.8} \]
\[ d_t = \sqrt{2 \times 6400 \times 33.8 \times 10^3} = \sqrt{432640 \times 10^3} \approx 657.8 \times 10^{1.5} \approx 657.8 \times 31.62 \approx 20800 \, m = 20.8 \, km \]
2. Calculate the distance contributed by the receiving antenna:
\[ d_r = \sqrt{2R h_r} = \sqrt{2 \times 6400 \times 10^3 \times 64.8} \]
\[ d_r = \sqrt{2 \times 6400 \times 64.8 \times 10^3} = \sqrt{829440 \times 10^3} \approx 910.8 \times 10^{1.5} \approx 910.8 \times 31.62 \approx 28800 \, m = 28.8 \, km \]
3. Sum the distances to get the maximum line of sight distance:
\[ d = d_t + d_r = 20.8 \, km + 28.8 \, km = 49.6 \, km \]
Final Answer:
The maximum distance between the antennas for satisfactory communication is:
\[ \boxed{49.6 \, km} \]
This corresponds to option (3). Quick Tip: When calculating the line of sight distance between antennas, remember to account for the heights of both antennas and use the Earth's radius in the formula.
Identify the pair of species having the same energy from the following: (The number given in the bracket corresponds to the principal quantum number (n) in which the electron is present.)
View Solution
To identify the pair of species having the same energy, we need to consider the energy levels of electrons in hydrogen-like species. The energy of an electron in a hydrogen-like species is given by:
\[ E_n = -\frac{13.6 \, eV \cdot Z^2}{n^2} \]
where:
- \( Z \) is the atomic number,
- \( n \) is the principal quantum number.
Analysis of Each Option:
1. Option (1): \( H(n=1), Li^{2+} (n=1) \)
- For \( H \) (Z = 1, n = 1):
\[ E_1 = -\frac{13.6 \cdot 1^2}{1^2} = -13.6 \, eV \]
- For \( Li^{2+} \) (Z = 3, n = 1):
\[ E_1 = -\frac{13.6 \cdot 3^2}{1^2} = -122.4 \, eV \]
- Energies are not the same.
2. Option (2): \( Li^{2+} (n=3), Be^{3+} (n=4) \)
- For \( Li^{2+} \) (Z = 3, n = 3):
\[ E_3 = -\frac{13.6 \cdot 3^2}{3^2} = -13.6 \, eV \]
- For \( Be^{3+} \) (Z = 4, n = 4):
\[ E_4 = -\frac{13.6 \cdot 4^2}{4^2} = -13.6 \, eV \]
- Energies are the same.
3. Option (3): \( He^+ (n=1), Li^{2+} (n=3) \)
- For \( He^+ \) (Z = 2, n = 1):
\[ E_1 = -\frac{13.6 \cdot 2^2}{1^2} = -54.4 \, eV \]
- For \( Li^{2+} \) (Z = 3, n = 3):
\[ E_3 = -\frac{13.6 \cdot 3^2}{3^2} = -13.6 \, eV \]
- Energies are not the same.
4. Option (4): \( H(n=3), Li^{2+} (n=2) \)
- For \( H \) (Z = 1, n = 3):
\[ E_3 = -\frac{13.6 \cdot 1^2}{3^2} = -1.51 \, eV \]
- For \( Li^{2+} \) (Z = 3, n = 2):
\[ E_2 = -\frac{13.6 \cdot 3^2}{2^2} = -30.6 \, eV \]
- Energies are not the same.
Final Answer:
- The pair of species having the same energy is:
\[ \boxed{Li^{2+} (n=3), Be^{3+} (n=4)} \]
This corresponds to option (2). Quick Tip: When dealing with hydrogen-like atoms, remember that the energy levels only depend on the atomic number \( Z \) and the principal quantum number \( n \).
Which one of the following corresponds to the wavelength of line spectrum of H atom in its Balmer series? (R = Rydberg constant)
View Solution
To determine which option corresponds to the wavelength of a line in the Balmer series of the hydrogen atom, we use the Rydberg formula for the Balmer series:
\[ \frac{1}{\lambda} = R \left( \frac{1}{2^2} - \frac{1}{n^2} \right) \]
where:
- \( \lambda \) is the wavelength,
- \( R \) is the Rydberg constant,
- \( n \) is an integer greater than 2 (since the Balmer series corresponds to transitions to the \( n=2 \) level).
Analysis of Each Option:
1. Option (1): \(\frac{9}{8R}\)
- Rearrange to find \( \lambda \):
\[ \lambda = \frac{9}{8R} \]
- Using the Rydberg formula:
\[ \frac{1}{\lambda} = \frac{8R}{9} = R \left( \frac{1}{4} - \frac{1}{n^2} \right) \]
\[ \frac{8}{9} = \frac{1}{4} - \frac{1}{n^2} \]
\[ \frac{1}{n^2} = \frac{1}{4} - \frac{8}{9} = \frac{9 - 32}{36} = -\frac{23}{36} \]
- This is not possible since \( \frac{1}{n^2} \) cannot be negative.
2. Option (2): \(\frac{100}{21R}\)
- Rearrange to find \( \lambda \):
\[ \lambda = \frac{100}{21R} \]
- Using the Rydberg formula:
\[ \frac{1}{\lambda} = \frac{21R}{100} = R \left( \frac{1}{4} - \frac{1}{n^2} \right) \]
\[ \frac{21}{100} = \frac{1}{4} - \frac{1}{n^2} \]
\[ \frac{1}{n^2} = \frac{1}{4} - \frac{21}{100} = \frac{25 - 21}{100} = \frac{4}{100} = \frac{1}{25} \]
\[ n^2 = 25 \implies n = 5 \]
- This is a valid transition (\( n=5 \) to \( n=2 \)).Option (2) is valid.
3. Option (3): \(\frac{25}{24R}\)
- Rearrange to find \( \lambda \):
\[ \lambda = \frac{25}{24R} \]
- Using the Rydberg formula:
\[ \frac{1}{\lambda} = \frac{24R}{25} = R \left( \frac{1}{4} - \frac{1}{n^2} \right) \]
\[ \frac{24}{25} = \frac{1}{4} - \frac{1}{n^2} \]
\[ \frac{1}{n^2} = \frac{1}{4} - \frac{24}{25} = \frac{25 - 96}{100} = -\frac{71}{100} \]
- This is not possible since \( \frac{1}{n^2} \) cannot be negative.
4. Option (4): \(\frac{16}{15R}\)
- Rearrange to find \( \lambda \):
\[ \lambda = \frac{16}{15R} \]
- Using the Rydberg formula:
\[ \frac{1}{\lambda} = \frac{15R}{16} = R \left( \frac{1}{4} - \frac{1}{n^2} \right) \]
\[ \frac{15}{16} = \frac{1}{4} - \frac{1}{n^2} \]
\[ \frac{1}{n^2} = \frac{1}{4} - \frac{15}{16} = \frac{4 - 15}{16} = -\frac{11}{16} \]
- This is not possible since \( \frac{1}{n^2} \) cannot be negative.
Final Answer:
The wavelength corresponding to a line in the Balmer series of the hydrogen atom is:
\[ \boxed{\frac{100}{21R}} \]
This corresponds to option (2). Quick Tip: The Balmer series corresponds to transitions where the electron falls to the \(n=2\) level.
Identify the pair of elements in which the number of s-electrons to p-electrons ratio is 2:3:
View Solution
Phosphorus (P) has the electronic configuration \( 1s^2 2s^2 2p^6 3s^2 3p^3 \), so it has 4 s-electrons and 3 p-electrons.
Calcium (Ca) has the electronic configuration \( 1s^2 2s^2 2p^6 3s^2 3p^6 4s^2 \), so it has 6 s-electrons and 6 p-electrons.
The ratio of s-electrons to p-electrons for the pair (P, Ca) is 2:3, making it the correct answer. Quick Tip: To find the ratio of s-electrons to p-electrons, count the total number of electrons in the respective orbitals for each element.
Which of the following has the least electron gain enthalpy?
View Solution
Electron gain enthalpy becomes more negative across a period and less negative down a group.
Oxygen and Sulphur belong to Group 16, but due to the smaller size of Oxygen, the added electron experiences greater repulsion, making its electron gain enthalpy less negative than Sulphur.
Among all options, Oxygen has the least electron gain enthalpy. Quick Tip: Smaller atoms tend to have less negative electron gain enthalpy due to stronger electron-electron repulsion.
According to Fajan’s rules, which of the following is not correct about covalent character?
View Solution
Fajan’s rule states that covalent character increases with smaller cation size and higher charge.
LiF should have more covalent character than KF, as Li\( ^+ \) has a higher charge density than K\( ^+ \).
The given statement "LiF \(<\) KF" is incorrect because LiF is more covalent than KF. Quick Tip: Covalent character increases with smaller cation size and larger anion size, as per Fajan’s rules.
Consider the following pairs:
(A) NO\(_2\) \(>\) O\(_3\) \(>\) H\(_2\)O (Bond angle)
(B) HF \(>\) H\(_2\)O \(>\) NH\(_3\) (Dipole moment)
(C) I\(_2\) \(>\) F\(_2\) \(>\) N\(_2\) (Bond length)
Which of the above pairs are correctly matched?
View Solution
(A) NO\(_2\) \(>\) O\(_3\) \(>\) H\(_2\)O (Bond angle): Correct, because NO\(_2\) has the least lone-pair repulsions, leading to a larger bond angle.
(B) HF \(>\) H\(_2\)O \(>\) NH\(_3\) (Dipole moment): Incorrect, because H\(_2\)O has a higher dipole moment than HF due to its bent structure.
(C) I\(_2\) \(>\) F\(_2\) \(>\) N\(_2\) (Bond length): Correct, because bond length increases with atomic size. Quick Tip: Bond angles are influenced by lone pairs and hybridization, while bond lengths depend on atomic size and bond order.
An open vessel containing air was heated from 27°C to 727°C. Some air was expelled. What is the fraction of air remaining in the vessel? (Assume air as an ideal gas)
View Solution
Using the ideal gas law, we know that the pressure and temperature are directly proportional when the volume is constant. The fraction of air remaining can be determined by comparing the initial and final temperatures:
\[ \frac{T_2}{T_1} = \frac{V_2}{V_1} \]
Where \( T_1 = 27^\circ C = 300K \) and \( T_2 = 727^\circ C = 1000K \). The fraction of air remaining is \( \frac{T_1}{T_2} \), which is \( \frac{7}{10} \). Quick Tip: In thermodynamics, the fraction of gas remaining can often be found by using the ideal gas law and considering the relationship between pressure, volume, and temperature.
12 g of an element reacts with 32 g of oxygen. What is the equivalent weight of the element?
View Solution
The equivalent weight of an element is calculated by dividing the molecular weight of the element by its valency. In this case, the molecular weight of the element is given as 12 g, and it reacts with 32 g of oxygen, which has a molecular weight of 32 g. The equivalent weight is:
\[ Equivalent weight = \frac{Molecular weight of element}{Valency} = \frac{12}{4} = 3 \] Quick Tip: To calculate the equivalent weight of an element, divide its molecular weight by its valency.
The standard enthalpy of formation (\(\Delta H_f^\circ\)) of ammonia is -46.2 kJ/mol. What is the \(\Delta H_f^\circ\) of the following reaction?
\[ N_2(g) + 3H_2(g) \rightarrow 2NH_3(g) \]
View Solution
For the reaction provided, the change in enthalpy can be calculated using Hess's Law. Given that the formation enthalpy of ammonia is -46.2 kJ/mol, and the reaction produces 2 moles of ammonia, the enthalpy change for the reaction is:
\[ \Delta H_f^\circ = 2 \times (-46.2) = -92.4 \, kJ/mol \]
Thus, the standard enthalpy of formation for this reaction is -92.4 kJ. Quick Tip: When using Hess's Law, remember that the enthalpy change for a reaction is the sum of the enthalpy changes for the formation of products and reactants.
At T(K), \(K_c\) for the reaction AO\(_2\)(g) + BO\(_2\)(g) \(\rightleftharpoons\) AO\(_3\)(g) + BO(g) is 16. One mole each of reactants and products are taken in a 1L flask and heated to T(K), and equilibrium is established. What is the equilibrium concentration of BO (in mol L\(^{-1}\))?
View Solution
Let the reaction be:
AO\(_2\)(g) + BO\(_2\)(g) \(\rightleftharpoons\) AO\(_3\)(g) + BO(g)
Initial concentrations:
[AO\(_2\)] = 1 mol/L
[BO\(_2\)] = 1 mol/L
[AO\(_3\)] = 1 mol/L
[BO] = 1 mol/L
Let x be the change in concentration at equilibrium.
Equilibrium concentrations:
[AO\(_2\)] = 1 - x
[BO\(_2\)] = 1 - x
[AO\(_3\)] = 1 + x
[BO] = 1 + x
The equilibrium constant \(K_c\) is given by: \[K_c = \frac{[AO_3][BO]}{[AO_2][BO_2]}\]
Given \(K_c = 16\), we have: \[16 = \frac{(1+x)(1+x)}{(1-x)(1-x)} = \left(\frac{1+x}{1-x}\right)^2\]
Taking the square root of both sides: \[4 = \frac{1+x}{1-x}\] \[4(1-x) = 1+x\] \[4 - 4x = 1 + x\] \[3 = 5x\] \[x = \frac{3}{5} = 0.6\]
The equilibrium concentration of BO is:
[BO] = 1 + x = 1 + 0.6 = 1.6 mol/L Quick Tip: Remember to set up an ICE table (Initial, Change, Equilibrium) to solve equilibrium problems.
Observe the following reactions:
\[ I. H_2O(l) + 2Na(s) \rightarrow 2NaOH(aq) + H_2(g) \] \[ II. 2H_2O(l) + 2F_2(g) \rightarrow 4H^+(aq) + 4F^-(aq) + O_2(g) \]
Identify the correct statement:
View Solution
To identify the correct statement about the reactions, we need to analyze the oxidation and reduction processes in each reaction.
Reaction I: \[ H_2O(l) + 2Na(s) \rightarrow 2NaOH(aq) + H_2(g) \]
Oxidation: Sodium (\(Na\)) is oxidized from \(0\) to \(+1\).
Reduction: Water (\(H_2O\)) is reduced. The hydrogen in \(H_2O\) goes from \(+1\) to \(0\) in \(H_2\).
Thus, in Reaction I, water is reduced.
Reaction II: \[ 2H_2O(l) + 2F_2(g) \rightarrow 4H^+(aq) + 4F^-(aq) + O_2(g) \]
Oxidation: Water (\(H_2O\)) is oxidized. The oxygen in \(H_2O\) goes from \(-2\) to \(0\) in \(O_2\).
Reduction: Fluorine (\(F_2\)) is reduced from \(0\) to \(-1\).
Thus, in Reaction II, water is oxidized.
Correct Statement:
In Reaction I, water is reduced.
In Reaction II, water is oxidized.
The correct option is: \[ \boxed{(3) In reaction I water is reduced and in reaction II water is oxidized.} \] Quick Tip: Oxidation is the loss of electrons, while reduction is the gain of electrons.
What is the correct stability order of \( KO_2, RbO_2, CsO_2 \)?
View Solution
To determine the correct stability order of \( KO_2 \), \( RbO_2 \), and \( CsO_2 \), we need to consider the stability of the superoxide ion (\( O_2^- \)) in these compounds. The stability of the superoxide ion is influenced by the size of the alkali metal cation. Larger cations stabilize the superoxide ion better due to lower charge density and weaker electrostatic attraction.
Stability Trend:
As we move down the alkali metal group (from \( K \) to \( Rb \) to \( Cs \)), the size of the cation increases.
Larger cations (like \( Cs^+ \)) stabilize the superoxide ion (\( O_2^- \)) more effectively than smaller cations (like \( K^+ \)).
Thus, the stability order of the superoxides is: \[ KO_2 < RbO_2 < CsO_2 \]
Correct Option:
The correct stability order is: \[ \boxed{KO_2 < RbO_2 < CsO_2} \]
This corresponds to option (4). Quick Tip: Superoxides contain \( O_2^- \) ions and are more stable with smaller cations due to better electrostatic interactions.
Assertion (A): \( MgO, CaO, SrO, \) and \( BaO \) are insoluble in water.
Reason (R): In aqueous medium, the basic strength of \( MgO, CaO, SrO, \) and \( BaO \) increases with increase in the atomic number of the metal.
The correct option among the following is
View Solution
Assertion (A): MgO, CaO, SrO, and BaO are insoluble in water.
This statement is not entirely correct. While MgO has very low solubility in water, the solubility of the oxides of alkaline earth metals generally increases as you go down the group. CaO, SrO, and BaO react with water to form their respective hydroxides, which are soluble to varying degrees.
Reason (R): In an aqueous medium, the basic strength of MgO, CaO, SrO, and BaO increases with an increase in the atomic number of the metal.
This statement is correct. As you move down the group in the periodic table, the size of the metal cation increases. This leads to a weaker attraction between the metal cation and the oxide ion (O²⁻), making it easier for the oxide to donate electrons and act as a base. Therefore, the basic strength of the oxides increases down the group.
Correct Option:
Since the assertion is not entirely correct, but the reason is correct, the answer is (4) (A) is not correct but (R) is correct. Explanation:
The solubility and basic strength of these oxides are related to the size and charge density of the metal cations. Smaller cations with higher charge density (like Mg²⁺) have a stronger attraction to the oxide ion, making the oxide less soluble and less basic. Larger cations with lower charge density (like Ba²⁺) have a weaker attraction to the oxide ion, making the oxide more soluble and more basic. Quick Tip: The solubility of metal oxides generally increases down the group due to decreasing lattice energy.
Identify the element for which \( +1 \) oxidation state is more stable than \( +3 \) oxidation state.
View Solution
To identify the element for which the \( +1 \) oxidation state is more stable than the \( +3 \) oxidation state, we need to consider the inert pair effect. The inert pair effect is observed in heavier elements of groups 13, 14, and 15, where the \( ns^2 \) electrons (where \( n \) is the principal quantum number) are less likely to participate in bonding, making the \( +1 \) oxidation state more stable than the \( +3 \) oxidation state.
Analysis of the Elements:
1. Ga (Gallium, Group 13):
- Gallium typically exhibits the \( +3 \) oxidation state, and the \( +1 \) oxidation state is less common and less stable.
2. Sn (Tin, Group 14):
- Tin can exhibit both \( +2 \) and \( +4 \) oxidation states. The \( +2 \) oxidation state becomes more stable for heavier elements due to the inert pair effect, but \( +1 \) is not a common oxidation state for tin.
3. Tl (Thallium, Group 13):
- Thallium is a heavy element in Group 13, and it exhibits the inert pair effect. The \( +1 \) oxidation state is more stable than the \( +3 \) oxidation state for thallium.
4. Ge (Germanium, Group 14):
- Germanium typically exhibits the \( +4 \) oxidation state, and the \( +2 \) oxidation state is less common. The \( +1 \) oxidation state is not stable for germanium.
Conclusion:
The element for which the \( +1 \) oxidation state is more stable than the \( +3 \) oxidation state is Thallium (Tl).
The correct option is: \[ \boxed{(3) Tl} \] Quick Tip: The inert pair effect stabilizes lower oxidation states in heavier group 13 and 14 elements.
Observe the oxides \( CO, B_2O_3, SiO_2, CO_2, Al_2O_3, PbO_2, Tl_2O_3 \). The number of acidic oxides in the list is:
View Solution
To determine the number of acidic oxides in the given list, we need to classify each oxide as acidic, basic, or amphoteric based on their chemical behavior.
Analysis of the Oxides:
1. \( CO \) (Carbon Monoxide):
- \( CO \) is a neutral oxide. It does not react with acids or bases to form salts.
2. \( B_2O_3 \) (Boron Oxide):
- \( B_2O_3 \) is an acidic oxide. It reacts with water to form boric acid (\( H_3BO_3 \)).
3. \( SiO_2 \) (Silicon Dioxide):
- \( SiO_2 \) is an acidic oxide. It reacts with bases to form silicates.
4. \( CO_2 \) (Carbon Dioxide):
- \( CO_2 \) is an acidic oxide. It reacts with water to form carbonic acid (\( H_2CO_3 \)).
5. \( Al_2O_3 \) (Aluminum Oxide):
- \( Al_2O_3 \) is an amphoteric oxide. It can react with both acids and bases.
6. \( PbO_2 \) (Lead Dioxide):
- \( PbO_2 \) is an amphoteric oxide. It can react with both acids and bases.
7. \( Tl_2O_3 \) (Thallium Oxide):
- \( Tl_2O_3 \) is a basic oxide. It reacts with acids to form salts.
Summary:
Acidic oxides: \( B_2O_3, SiO_2, CO_2 \) (3 oxides).
Neutral oxide: \( CO \) (1 oxide).
Amphoteric oxides: \( Al_2O_3, PbO_2 \) (2 oxides).
Basic oxide: \( Tl_2O_3 \) (1 oxide).
Number of Acidic Oxides:
There are 3 acidic oxides in the list.
The correct option is: \[ \boxed{(1) 3} \] Quick Tip: Acidic oxides are typically non-metallic oxides, while amphoteric oxides can act as both acids and bases.
The common components of photochemical smog are:
View Solution
Photochemical smog is formed by the reaction of sunlight with pollutants such as nitrogen oxides and volatile organic compounds. The most common components of photochemical smog are ozone (\( O_3 \)), nitrogen oxides (\( NO \)), and peroxyacetyl nitrates (PAN), which are formed under high-temperature conditions, especially in the presence of sunlight. Quick Tip: Photochemical smog is a complex mixture of pollutants that forms when sunlight reacts with pollutants such as NO and hydrocarbons. Ozone is a key component.
The electron displacement effect observed in the given structures is known as:
View Solution
In the given structure, the electron displacement observed is due to the withdrawal of electron density from the benzene ring to the substituent group, leading to a -R effect (resonance withdrawing effect). This effect reduces the electron density in the aromatic ring, making it more reactive toward electrophiles. Quick Tip: The -R effect is observed when a substituent group withdraws electron density from the rest of the molecule through resonance. This effect stabilizes positive charges but destabilizes negative charges.
An alkene X (C\(_4\)H\(_8\)) exhibits geometrical isomerism. Oxidation of X with KMnO\(_4\)/H\(^+\) gave Y. On heating sodium salt of Y with a mixture of NaOH and CaO gave Z. What is Z?
View Solution
An alkene that exhibits geometrical isomerism must have a carbon-carbon double bond, with each of the two carbons in the double bond attached to two different groups. Of the alkenes with formula C\(_4\)H\(_8\), only 2-butene exhibits geometrical isomerism: \[CH_3 CH = CHCH_3.\]Oxidation of an alkene with KMnO\(_4\)/H\(^+\) cleaves the double bond, and converts each carbon in the double bond to a carbonyl group. Thus, Y is \[CH_3 COOH.\]Heating the sodium salt of a carboxylic acid with a mixture of NaOH and CaO produces an alkane with one fewer carbon atom. This reaction is called the decarboxylation reaction. Thus, Z is CH\(_4\). Quick Tip: The decarboxylation reaction removes a carbon atom from a carboxylic acid, producing an alkane.
The number of activating and deactivating groups of the following are respectively:
\[ -OCH_2CH_3, -COCH_3, -NHCOCH_3, -COOCH_3, -SO_3H \]
View Solution
Activating groups: Electron-donating groups increase reactivity, such as -OCH2CH3 and -NHCOCH3.
Deactivating groups: Electron-withdrawing groups decrease reactivity, such as -COCH3, -COOCH3, and -SO3H.
Thus, the number of activating groups = 2 and deactivating groups = 3. Quick Tip: Activating groups donate electrons and increase electrophilic substitution, while deactivating groups withdraw electrons and reduce reactivity.
X and Z respectively in the following reaction sequence are:
\[ C_3H_6 \xrightarrow{X} Y \xrightarrow{C_6H_6/AlCl_3} Z \]
View Solution
Step 1: Propene (\( C_3H_6 \)) reacts with HBr in the presence of ROOR to form 1-bromopropane via anti-Markovnikov addition.
Step 2: 1-bromopropane undergoes Friedel-Crafts alkylation with benzene and AlCl3, forming n-propylbenzene.
Thus, the correct sequence is HBr/ROOR. Quick Tip: Peroxides lead to anti-Markovnikov addition of HBr, forming 1-bromopropane instead of 2-bromopropane.
The molecular formula of a compound is \( AB_2O_4 \). Atoms of O form a ccp lattice.
Atoms of A (cation) occupy \( \frac{1}{8} \) of tetrahedral voids. Atoms of B (cation) occupy a fraction of octahedral voids. What is the fraction of vacant octahedral voids?
View Solution
To solve this problem, we need to analyze the crystal structure of the compound \( AB_2O_4 \) and determine the fraction of vacant octahedral voids.
Step 1: Understand the Structure
The oxygen atoms (\( O \)) form a ccp (cubic close-packed) lattice.
In a ccp lattice, there are 4 oxygen atoms per unit cell.
The formula of the compound is \( AB_2O_4 \), which means:
\( A \) cations: 1 per unit cell,
\( B \) cations: 2 per unit cell,
\( O \) anions: 4 per unit cell.
Step 2: Tetrahedral and Octahedral Voids
In a ccp lattice:
The number of tetrahedral voids = \( 2 \times number of atoms = 2 \times 4 = 8 \).
The number of octahedral voids = \( number of atoms = 4 \).
Step 3: Occupancy of Voids
Tetrahedral voids:
Atoms of \( A \) occupy \( \frac{1}{8} \) of the tetrahedral voids.
Total tetrahedral voids = 8.
Occupied tetrahedral voids = \( \frac{1}{8} \times 8 = 1 \).
Vacant tetrahedral voids = \( 8 - 1 = 7 \).
Octahedral voids:
Atoms of \( B \) occupy a fraction of the octahedral voids.
Total octahedral voids = 4.
From the formula \( AB_2O_4 \), there are 2 \( B \) cations per unit cell.
Occupied octahedral voids = 2.
Vacant octahedral voids = \( 4 - 2 = 2 \).
Step 4: Fraction of Vacant Octahedral Voids
Total octahedral voids = 4.
Vacant octahedral voids = 2.
Fraction of vacant octahedral voids = \( \frac{2}{4} = \frac{1}{2} \).
Final Answer:
The fraction of vacant octahedral voids is: \[ \boxed{\frac{1}{2}} \]
This corresponds to option (4). Quick Tip: In CCP lattices, tetrahedral voids are twice the number of atoms, and octahedral voids are equal to the number of atoms.
Distilled water boils at 373.15 K and freezes at 273.15 K. A solution of glucose in distilled water boils at 373.202 K. What is the freezing point (in K) of the same solution?
(For water, \( K_b = 0.52 \) kg mol\(^{-1}\), \( K_f = 1.86 \) kg mol\(^{-1}\))
View Solution
- The boiling point elevation is:
\[ \Delta T_b = i K_b m \]
\[ 0.052 = (1)(0.52) m \]
\[ m = 0.1 mol/kg \]
- The freezing point depression is:
\[ \Delta T_f = i K_f m \]
\[ \Delta T_f = (1)(1.86)(0.1) = 0.186 \]
\[ T_f = 273.15 - 0.186 = 272.964 K \] Quick Tip: Boiling point elevation and freezing point depression depend on molality and colligative properties.
Identify the correct statements from the following:
A) At 298 K, the potential of the hydrogen electrode placed in a solution of pH = 10 is -0.59 V.
B) The limiting molar conductivity of \( Ca^{2+} \) and \( Cl^- \) is 119 and 76 \( S cm^2 mol^{-1} \), respectively. The limiting molar conductivity of \( CaCl_2 \) is 195 \( S cm^2 mol^{-1} \).
C) The correct relationship between \( K_c \) and \( E_{cell} \) is \( E_{cell} = \frac{2.303RT}{nF} \log K_c \).
View Solution
A) The potential of the hydrogen electrode in a solution with pH = 10 is correctly calculated using the Nernst equation, resulting in -0.59 V.
B) The limiting molar conductivities of \( Ca^{2+} \) and \( Cl^- \) are correctly stated, but the limiting conductivity of \( CaCl_2 \) is actually 195 \( S cm^2 mol^{-1} \).
C) The relationship between the equilibrium constant \( K_c \) and the cell potential \( E_{cell} \) is correctly expressed as \( E_{cell} = \frac{2.303RT}{nF} \log K_c \). Quick Tip: For electrochemical reactions, the relationship between the cell potential and the equilibrium constant is governed by the Nernst equation, which can help determine the direction of the reaction.
For a first-order reaction, a plot of \( \ln k \) (y-axis) and \( \frac{1}{T} \) (x-axis) gave a straight line with a slope equal to \( -10^4 \) and an intercept equal to 2.303 (on the y-axis). What is the activation energy \( E_a \) (in kJ/mol) of the reaction?
(Given \( R = 8.314 \, J mol^{-1} K^{-1} \))
View Solution
The Arrhenius equation is given by:
\(\)k = Ae^{-\frac{E_a{RT\(\)
Taking the natural logarithm of both sides, we get:
\(\)\ln k = \ln A - \frac{E_a{RT\(\)
Comparing this equation with the equation of a straight line, \(y = mx + c\), where \(y = \ln k\) and \(x = \frac{1}{T}\), we can see that:
Slope (m) = \(-\frac{E_a}{R}\)
Intercept (c) = \(\ln A\)
Given:
Slope = \(-10^3\) K
Intercept = 2.303
R = 8.314 J mol\(^{-1}\) K\(^{-1}\)
We have:
\(\)-\frac{E_a{R = -10^3\(\)
\(\)E_a = R \times 10^3\(\)
\(\)E_a = 8.314 J mol^{-1 \text{K^{-1 \times 10^3 \text{ K\(\)
\(\)E_a = 8314 \text{ J mol^{-1\(\)
To convert J mol\(^{-1\) to kJ mol\(^{-1}\), we divide by 1000:
\(\)E_a = \frac{8314{1000 kJ mol^{-1\(\)
\(\)E_a = 8.314 \text{ kJ mol^{-1\(\)
Therefore, the activation energy (\(E_a\)) of the reaction is 8.314 kJ mol\(^{-1\).
Final Answer:
The final answer is \(\boxed{8.314}\) Quick Tip: The slope of the \( \ln k \) vs. \( \frac{1}{T} \) plot is used to calculate the activation energy of a reaction using the Arrhenius equation.
Adsorption of a gas (A) on an adsorbent follows Freundlich adsorption isotherm. The slope and intercept (on y-axis) of the isotherm are 0.5 and 1.0, respectively. What is the value of \( \frac{x}{m} \), when the pressure of the gas (A) is 100 atm?
View Solution
To solve this problem, we will use the Freundlich adsorption isotherm, which is given by:
\[ \frac{x}{m} = k \cdot P^{1/n} \]
where:
- \( \frac{x}{m} \) is the amount of gas adsorbed per unit mass of the adsorbent,
- \( P \) is the pressure of the gas,
- \( k \) and \( n \) are constants.
Step 1: Freundlich Isotherm in Logarithmic Form
The Freundlich isotherm can be expressed in logarithmic form as:
\[ \log \left( \frac{x}{m} \right) = \log k + \frac{1}{n} \log P \]
This is a linear equation of the form \( y = mx + c \), where:
- \( y = \log \left( \frac{x}{m} \right) \),
- \( m = \frac{1}{n} \) (slope),
- \( c = \log k \) (intercept).
Step 2: Given Data
- Slope (\( \frac{1}{n} \)) = 0.5,
- Intercept (\( \log k \)) = 1.0,
- Pressure (\( P \)) = 100 atm.
Step 3: Calculate \( n \) and \( k \)
From the slope: \[ \frac{1}{n} = 0.5 \implies n = 2 \]
From the intercept: \[ \log k = 1.0 \implies k = 10^1 = 10 \]
Step 4: Calculate \( \frac{x}{m} \)
Using the Freundlich isotherm: \[ \frac{x}{m} = k \cdot P^{1/n} \]
Substitute the values: \[ \frac{x}{m} = 10 \cdot (100)^{1/2} \]
Simplify: \[ \frac{x}{m} = 10 \cdot 10 = 100 \]
Final Answer:
The value of \( \frac{x}{m} \) is: \[ \boxed{100} \]
This corresponds to option (2). Quick Tip: For the Freundlich adsorption isotherm, the value of \( \frac{x}{m} \) can be calculated by using the slope and intercept from the graph of \( \log \left( \frac{x}{m} \right) \) vs. \( \log P \).
A low boiling point metal contains high boiling point metal as impurity. The correct refining method is
View Solution
Distillation is a separation technique based on differences in boiling points. In this case, since the metal has a low boiling point and the impurity has a high boiling point, distillation is the appropriate method. The low boiling point metal will vaporize, leaving the high boiling point impurity behind.
Liquation is used to separate metals with low melting points from those with higher melting points. Poling is used to purify metals that contain metal oxides as impurities. Vapour phase refining is used to purify metals by converting them into a volatile compound, which is then decomposed to give the pure metal. Quick Tip: Distillation is effective when the boiling points of the components are significantly different.
Which of the following when subjected to thermal decomposition will liberate dinitrogen?
(i) sodium nitrate
(ii) ammonium dichromate
(iii) barium azide
View Solution
Ammonium dichromate (\( (NH_4)_2Cr_2O_7 \)) decomposes to form N\(_2\), Cr\(_2O_3\), and H\(_2\)O.
Barium azide (Ba(N\(_3\))\(_2\)) decomposes to give Ba and N\(_2\) gas.
Sodium nitrate (NaNO\(_3\)) decomposes into NaNO\(_2\) and O\(_2\), not N\(_2\). Quick Tip: Compounds containing azide (\( N_3^- \)) or ammonium cation (\( NH_4^+ \)) tend to release nitrogen gas upon decomposition.
Observe the following reaction. This reaction represents:
\[ 4HCl + O_2 \xrightarrow{CuCl_2, 723K} 2Cl_2 + 2H_2O \]
View Solution
The Deacon’s process is used for the industrial production of chlorine gas.
In this reaction, HCl is oxidized by oxygen in the presence of CuCl\(_2\) catalyst at 723K to produce Cl\(_2\) and H\(_2\)O. Quick Tip: Deacon’s process is an industrial method used for producing chlorine gas from HCl.
Identify the set which is not correctly matched in the following:
View Solution
Neon (Ne) is an inert, colorless, and odorless gas. The description of "fluorescent green gas, rotten egg smell" is incorrect.
PH\(_3\) has a rotten fish smell, Cl\(_2\) is greenish yellow and pungent, and SO\(_2\) is colorless with a pungent smell, all of which are correctly matched. Quick Tip: Noble gases like neon are colorless and odorless, unlike other reactive gases.
Identify the correct statements from the following:
(i) Ti (IV) is more stable than Ti (III) and Ti (II)
(ii) Among 3d-series elements (from Z = 22 to 29) only copper has positive reduction potential (\( M^{2+}/M \))
(iii) Both Sc and Zn exhibit +1 oxidation state
View Solution
(i) True: Titanium(IV) is the most stable oxidation state of titanium due to its noble gas-like electronic configuration.
(ii) True: Among 3d-series elements, only copper (Cu) has a positive standard reduction potential, making it unique.
(iii) False: Scandium (Sc) and Zinc (Zn) do not exhibit a stable +1 oxidation state; Sc commonly shows +3, and Zn shows +2. Quick Tip: Titanium prefers the +4 oxidation state due to noble gas configuration, and Cu is unique in its positive reduction potential.
The molecular formula of a coordinate complex is CoH\(_{12}\)O\(_6\)Cl\(_3\). When one mole of this aqueous solution of complex is reacted with excess of aqueous AgNO\(_3\) solution, three moles of AgCl were formed. What is the correct formula of the complex?
View Solution
When one mole of the given complex reacts with excess AgNO\(_3\) solution, three moles of AgCl are formed. This suggests that the complex contains three chloride ions. The correct formula of the complex is [Co(H\(_2\)O)\(_6\)]Cl\(_3\), where Co is coordinated to six water molecules, with three chloride ions as counterions. Quick Tip: When determining the formula of a complex, consider the stoichiometry of the reaction with other compounds (like AgNO\(_3\)) to identify the number of ligands and counterions.
Match the following:
The correct answer is:
View Solution
Let's analyze each monomer and match it with the correct polymer:
A. CF\(_2\)=CF\(_2\) (Tetrafluoroethylene) is the monomer used to produce Teflon.
B. NH\(_2\)(CH\(_2\))\(_6\)NH\(_2\) (Hexamethylenediamine) and HO\(_2\)C(CH\(_2\))\(_4\)CO\(_2\)H (Adipic acid) are the monomers used to produce Nylon 6,6.
C. C\(_6\)H\(_5\)OH (Phenol) and HCHO (Formaldehyde) are the monomers used to produce Bakelite.
D. CH\(_2\)=CH(Cl)-CH=CH\(_2\) (Chloroprene) is the monomer used to produce Neoprene.
Therefore, the correct matching is:
A - III (Teflon)
B - IV (Nylon 6,6)
C - II (Bakelite)
D - I (Neoprene)
Final Answer: (2) A-III; B-IV; C-II; D-I Quick Tip: Polymerization reactions involve the combination of monomers, often creating polymers with distinct physical properties.
The functional groups involved in the conversion of glucose to gluconic acid and gluconic acid to saccharic acid respectively are:
View Solution
Glucose is an aldohexose, which means it has an aldehyde functional group (-CHO) and six carbon atoms. Gluconic acid is obtained by the oxidation of the aldehyde group in glucose to a carboxylic acid group (-COOH).
Saccharic acid is a dicarboxylic acid, which means it has two carboxylic acid groups. It is obtained by the further oxidation of gluconic acid. In this oxidation, the primary alcohol group (-CH\(_2\)OH) at the other end of the molecule is oxidized to a carboxylic acid group.
Therefore, the functional groups involved in the conversion of glucose to gluconic acid and gluconic acid to saccharic acid are -CHO and -CH\(_2\)OH, respectively. Quick Tip: Oxidation reactions often involve the conversion of aldehyde groups to carboxylic acids, which is seen in the conversion of glucose to gluconic acid and further to saccharic acid.
Among the following, the incorrect statement about chloramphenicol is:
View Solution
Chloramphenicol is a bacteriostatic drug, meaning it inhibits the growth of bacteria but does not directly kill them. It is a broad-spectrum antibiotic used to treat a variety of bacterial infections, including typhoid fever. Quick Tip: Bacteriostatic drugs inhibit bacterial growth, while bactericidal drugs directly kill bacteria. Chloramphenicol is an example of a bacteriostatic drug.
A halogen compound X (C\(_4\)H\(_9\)Br) on hydrolysis gave alcohol Y. The alcohol Y undergoes dehydration with 20% H\(_3\)PO\(_4\) at 358 K. What is X?
View Solution
The halogen compound (CH\(_3\))\(_3\)CBr undergoes SN1 hydrolysis to form tertiary butanol.
This tertiary butanol dehydrates with H\(_3\)PO\(_4\) to give 2-methylpropene, following a carbocation mechanism.
Thus, (CH\(_3\))\(_3\)CBr is the correct halogen compound. Quick Tip: Tertiary alkyl halides undergo SN1 reactions, forming stable carbocations, which easily dehydrate under acidic conditions.
An alcohol X (C\(_5\)H\(_{12}\)O) when reacted with conc. HCl and anhydrous ZnCl\(_2\), produces turbidity instantly. The alcohol X can be prepared from which of the following reactions?
View Solution
The Lucas test (reaction with HCl/ZnCl\(_2\)) gives instant turbidity for tertiary alcohols.
The acid-catalyzed hydration of 2-methyl-1-butene forms 2-methyl-2-butanol, a tertiary alcohol, which reacts instantly.
Other options do not form tertiary alcohols. Quick Tip: Tertiary alcohols react instantly with Lucas reagent due to rapid formation of carbocations.
Assertion (A): Chlorobenzene is not formed in the reaction of phenol with thionyl chloride.
Reason (R): In phenol, carbon–oxygen bond has partial double bond character.
View Solution
Phenol does not react with SOCl\(_2\) because the C–O bond in phenol has partial double bond character due to resonance.
This prevents the replacement of –OH with –Cl, unlike in aliphatic alcohols.
Since resonance explains the non-reactivity, (R) correctly explains (A). Quick Tip: Phenol’s C–O bond is strengthened by resonance, making it resistant to nucleophilic substitution.
The pK\(_a\) values of X, Y, Z respectively are 8.3, 7.1, 10.2. What are X, Y, Z?
View Solution
The given pK\(_a\) values can be associated with the strength of acids. A lower pK\(_a\) value indicates a stronger acid. By analyzing the structures and comparing their acid strengths, we can conclude that the correct structures corresponding to the given pK\(_a\) values are represented by Structure 1. Quick Tip: In organic chemistry, pK\(_a\) values are used to compare the strength of acids. A lower pK\(_a\) indicates a stronger acid, meaning it dissociates more readily in solution.
The reagents/ chemicals X and Y that convert cyanobenzene to Schiff's base are
View Solution
A Schiff base is a compound with the general structure R\(_1\)R\(_2\)C=NR\(_3\), where R\(_3\) is an aryl or alkyl group, but not a hydrogen. They are formed by the reaction of a primary amine with an aldehyde or ketone.
Cyanobenzene has the structure \[C_6 H_5 C \equiv N.\]Diisobutylaluminium hydride (DIBAL-H) is a reducing agent. It will reduce the nitrile group (-C\( \equiv \)N) in cyanobenzene to an imine group (-CH=NH): \[C_6 H_5 C \equiv N \xrightarrow{DIBAL-H, H_2 O} C_6 H_5 CH = NH.\]Then, the imine will react with aniline (C\(_6\)H\(_5\)NH\(_2\)) to form a Schiff base: \[C_6 H_5 CH = NH + C_6 H_5 NH_2 \rightarrow C_6 H_5 CH = N C_6 H_5 + NH_3.\] Quick Tip: DIBAL-H is a useful reagent for reducing nitriles to imines.
The correct statements of the following are:
A) Aniline forms a stable benzene diazonium chloride at 285K.
B) N - Phenylethanamide is less reactive towards nitration than aniline.
C) p - CH\(_3\)C\(_6\)H\(_4\)COCl is Hinsberg reagent.
View Solution
Let's analyze each statement:
A) Aniline forms a stable benzene diazonium chloride at 285K.
Benzene diazonium chloride is stable at low temperatures (0-5°C or 273-278K). At 285K, it would decompose. So statement A is incorrect.
B) N-Phenylethanamide is less reactive towards nitration than aniline.
N-Phenylethanamide (acetanilide) is less reactive towards electrophilic substitution reactions like nitration compared to aniline. This is because the lone pair of electrons on the nitrogen atom in acetanilide is delocalized over the carbonyl group, making it less available for donation to the benzene ring. Thus, statement B is correct.
C) p-CH\(_3\)C\(_6\)H\(_4\)COCl is Hinsberg reagent.
Hinsberg reagent is benzenesulfonyl chloride (C\(_6\)H\(_5\)SO\(_2\)Cl). p-CH\(_3\)C\(_6\)H\(_4\)COCl is not Hinsberg reagent. Thus, statement C is incorrect.
Therefore, the only correct statement is B.
Final Answer: (3) B only Quick Tip: The Hinsberg test involves the reaction of amines with benzoyl chloride (p - CH\(_3\)C\(_6\)H\(_4\)COCl) to distinguish between primary, secondary, and tertiary amines based on the solubility of the products.





































































































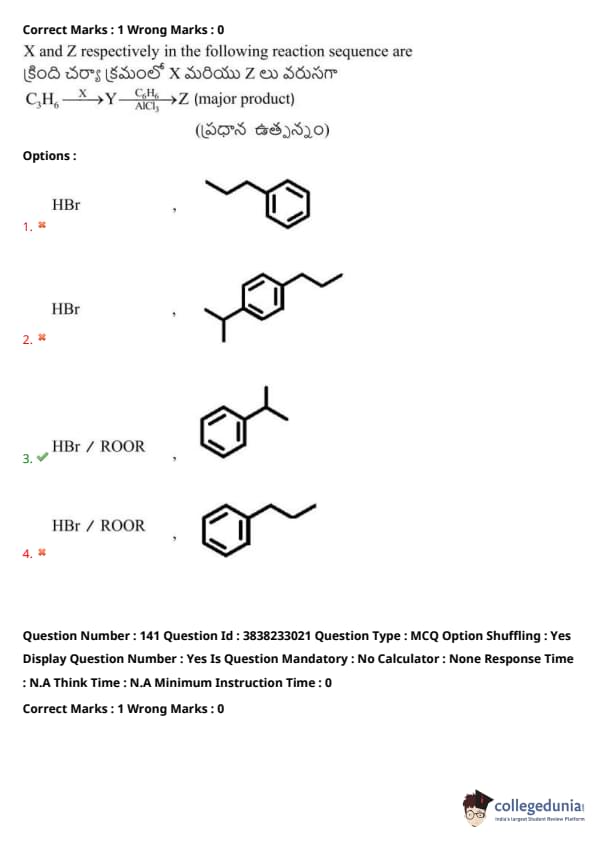














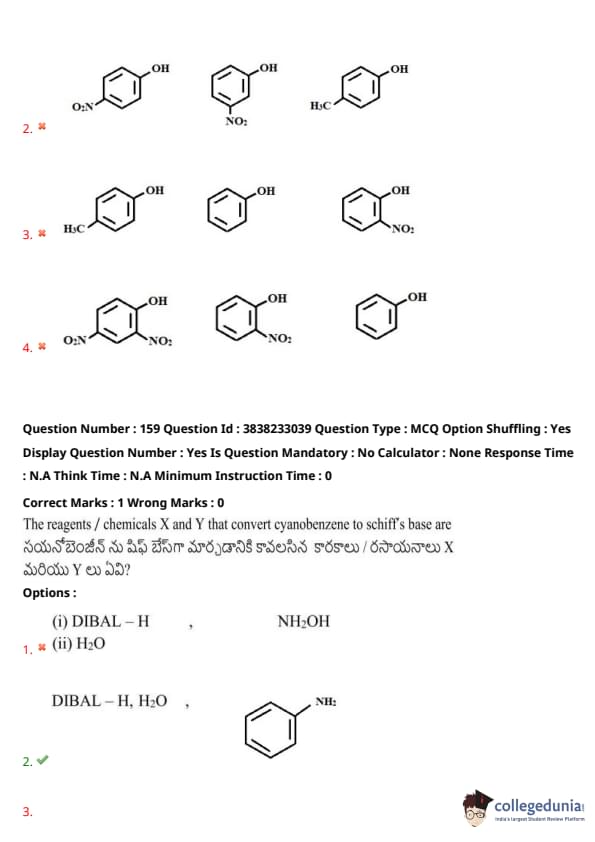


Also Check:
TS EAMCET Previous Year Question Papers
| TS EAMCET 2023 Question Paper | TS EAMCET 2022 Question Paper |
| TS EAMCET 2021 Question Paper | TS EAMCET 2020 Question Paper |
| TS EAMCET 2019 Question Paper | TS EAMCET 2018 Question Paper |
Also Check:







Comments