TS EAMCET 2024 Question Paper May 11 Shift 1: Download MPC Question Paper with Solutions PDF
TS EAMCET 2024 Question Paper May 11 Shift 1 with Answer Key PDF is available here for download. JNTU, Hyderabad on behalf of TSCHE conducted TS EAMCET on May 11 from 9 AM to 12 PM. TS EAMCET 2024 Question Paper consists of 160 questions carrying 1 mark each. TS EAMCET 2024 Question Paper May 11 Shift 1 PDF for MPC includes three subjects, Physics, Chemistry and Mathematics. The Physics and Chemistry section of the paper includes 40 questions each while the Mathematics section includes a total of 80 questions.
TS EAMCET 2024 Question Paper with Answer Key May 11 Shift 1 PDF
| TS EAMCET 2024 11 May Shift 1 Question Paper with Answer Key | Check Solution |
TS EAMCET Questions with Solution
If \(f(x)\) is a quadratic function such that \(f\left(\frac{1}{x}\right) = f(x) + f\left(\frac{1}{1-x}\right)\), then \(\sqrt{f\left(\frac{2}{3}\right) + f\left(\frac{3}{2}\right)} =\)
View Solution
If \( f(x) = ax^2 + bx + c \) is an even function and \( g(x) = px^3 + qx^2 + rx \) is an odd function, and if \( h(x) = f(x) + g(x) \) and \( h(-2) = 0 \), then \( 8p + 4q + 2r = \)?
View Solution
If \(1\cdot3\cdot5 + 3\cdot5\cdot7 + 5\cdot7\cdot9 + \ldots\) to \(n\) terms is \(n(n+1)f(n)\), then \(f(2) =\)
View Solution
Given matrices \( A = \begin{bmatrix} 1 & 2
2 & 1 \end{bmatrix} \) and \( B = \begin{bmatrix} x & y
1 & 2 \end{bmatrix} \), where \((A + B)(A - B) = A^2 - B^2\). If \( C = \begin{bmatrix} x & 2
1 & y \end{bmatrix} \), then the trace of \( C \) is:
View Solution
If \( x = k \) satisfies the equation \( \begin{vmatrix} x-2 & 3x-3 & 5x-5
x-4 & 3x-9 & 5x-25
x-8 & 3x-27 & 5x-125 \end{vmatrix} = 0 \), then \( x = k \) also satisfies the equation:
View Solution
If \(A\) is a non singular matrix, then \(Adj(A^{-1}) =\)
View Solution
If the homogeneous system of linear equations \(x - 2y + 3z = 0\), \(2x + 4y - 5z = 0\), \(3x + \lambda y + \mu z = 0\) has a non-trivial solution, then \(8\mu + 11\lambda =\)
View Solution
If \( z = \frac{(2-i)(1+i)^3}{(1-i)^2} \), then \(Arg(z) =\)
View Solution
If \( z = x + iy \) and the point \( P \) represents \( z \) in the Argand plane. If the amplitude of \( \frac{2z-i}{z+2i} \) is \( \frac{\pi}{4} \), then the equation of the locus of \( P \) is:
View Solution
If \( \alpha, \beta \) are the roots of the equation \( x^2 + 2x + 4 = 0 \). If the point representing \( \alpha \) in the Argand diagram lies in the 2nd quadrant and \( \alpha^{2024} - \beta^{2024} = ik \), where \( i = \sqrt{-1} \), then \( k = \)
View Solution
If \( \alpha \) is a root of the equation \( x^2 - x + 1 = 0 \), then \(\left(\alpha + \frac{1}{\alpha}\right)^3 + \left(\alpha^2 + \frac{1}{\alpha^2}\right)^3 + \left(\alpha^3 + \frac{1}{\alpha^3}\right)^3 + \left(\alpha^4 + \frac{1}{\alpha^4}\right)^3 =\)
View Solution
If \( \alpha, \beta \) are the real roots of the equation \( x^2 + ax + b = 0 \). If \( \alpha + \beta = \frac{1}{2} \) and \( \alpha^3 + \beta^3 = \frac{37}{8} \), then \( {a}-{\frac{1}{b}} =\)
View Solution
The solution set of the inequality \( \sqrt{x^2 + x - 2} > (1 - x) \) is:
View Solution
If \( \alpha, \beta, \gamma \) are the roots of the equation \( 4x^3 - 3x^2 + 2x - 1 = 0 \), then \( \alpha^3 + \beta^3 + \gamma^3 = \)
View Solution
The equation \( 16x^4 + 16x^3 - 4x - 1 = 0 \) has a multiple root. If \( \alpha, \beta, \gamma, \delta \) are the roots of this equation, then \( \frac{1}{\alpha^4} + \frac{1}{\beta^4} + \frac{1}{\gamma^4} + \frac{1}{\delta^4} = \)
View Solution
The sum of all the 4-digit numbers formed by taking all the digits from 0, 3, 6, 9 without repetition is:
View Solution
The number of ways in which 6 distinct things can be distributed into 2 boxes so that no box is empty is:
View Solution
The number of ways in which the number 831600 can be split into two factors which are relatively prime is:
View Solution
The coefficient of \(xy^2z^3\) in the expansion of \((x - 2y + 3z)^6\) is:
View Solution
The set of all real values of \(x\) for which the expansion of \( \left( 125x^2 - \frac{27}{x} \right)^{\frac{-2}{3}} \) is valid, is:
View Solution
If \(\frac{x^2}{2x^2 + 7x + 6} = \frac{Ax + B}{x^2 + a} + \frac{Cx + D}{ax^2 + 3}\), then \(A + B + C - 2D =\)
View Solution
Given \((\sin \theta - \csc \theta)^2 + (\cos \theta + \sec \theta)^2 = 5\) and \(\theta\) lies in the third quadrant, find \((\sin \theta + \cos \theta)^3\).
View Solution
Given \( \cos B - \sin A = \frac{\sqrt{3}+1}{4\sqrt{2}} \) and \( 2 \cos A \cos B = \frac{1+\sqrt{2}+\sqrt{3}}{2\sqrt{2}} \), calculate \( \cos^2 \frac{4B}{3} - \sin^2 \frac{4A}{5} \):
View Solution
If \( \theta \) is an acute angle and \( 2\sin^2 \theta = \cos^4 \frac{\pi}{8} + \sin^4 \frac{3\pi}{8} + \cos^4 \frac{5\pi}{8} + \sin^4 \frac{7\pi}{8} \), then \( \theta \) is:
View Solution
If \(2 \tan^2 \theta - 4 \sec \theta + 3 = 0\), then \(2 \sec \theta\) is:
View Solution
If \( \sin^{-1} x - \cos^{-1} 2x = \sin^{-1} \left(\frac{\sqrt{3}}{2}\right) - \cos^{-1} \left(\frac{\sqrt{3}}{2}\right) \), then \( \tan^{-1} x + \tan^{-1} \left(\frac{x}{x+1}\right) = \)
View Solution
If \( sech^{-1}\left(\frac{3}{5}\right) - tanh^{-1}\left(\frac{3}{5}\right) = \)
View Solution
In a triangle ABC, if \(a = 5\), \(b = 3\), and \(c = 7\), then the ratio \(\sqrt{\frac{\sin(A-B)}{\sin(A+B)}}\) is:
View Solution
In a triangle ABC, if \( r_1 = 6 \), \( r_2 = 9 \), \( r_3 = 18 \), then \( \cos A \) is:
View Solution
Given the position vectors of points \(A\) and \(B\) as \( \mathbf{A} = 2\mathbf{i} - 3\mathbf{j} + \mathbf{k} \) and \( \mathbf{B} = \mathbf{i} + 2\mathbf{j} - 3\mathbf{k} \), and \(C\) divides \(AB\) in the ratio 3:2. If \( \mathbf{D} = 3\mathbf{i} - \mathbf{j} + 2\mathbf{k} \) is the position vector of point \(D\), find the unit vector in the direction of \( \mathbf{CD} \):
View Solution
Given the position vectors of points \(A\) and \(B\) as \( \mathbf{A} = 2\mathbf{i} - 3\mathbf{j} + \mathbf{k} \) and \( \mathbf{B} = \mathbf{i} + 2\mathbf{j} - 3\mathbf{k} \), and \(C\) divides \(AB\) in the ratio 3:2. If \( \mathbf{D} = 3\mathbf{i} - \mathbf{j} + 2\mathbf{k} \) is the position vector of point \(D\), find the unit vector in the direction of \( \mathbf{CD} \):
View Solution
A unit vector \( \mathbf{e} = a\mathbf{i} + b\mathbf{j} + c\mathbf{k} \) is coplanar with the vectors \( \mathbf{i} - 3\mathbf{j} + 5\mathbf{k} \) and \( 3\mathbf{i} + \mathbf{j} - 5\mathbf{k} \) and is perpendicular to the vector \( \mathbf{i} + \mathbf{j} + \mathbf{k} \). Calculate \(2a^2 + 3b^2 + 4c^2\):
View Solution
Given vectors \( \mathbf{a} = \mathbf{i} + \mathbf{j} - 2\mathbf{k} \), \( \mathbf{b} = \mathbf{i} - 2\mathbf{j} + \mathbf{k} \), and \( \mathbf{c} = 2\mathbf{i} + \mathbf{j} - \mathbf{k} \). If \( \mathbf{d} \) is a normal to the plane of \( \mathbf{a} \) and \( \mathbf{b} \) and satisfies \( \mathbf{d} \cdot \mathbf{c} = 2 \), find the magnitude of \( \mathbf{d} \):
View Solution
Given two planes with equations \( \mathbf{r} \cdot (\mathbf{i} - \mathbf{j} + \mathbf{k}) = 5 \) and \( \mathbf{r} \cdot (2\mathbf{i} + \mathbf{j} - \mathbf{k}) = 3 \). A plane \( \pi \) passing through the line of intersection of these two planes also passes through the point (0,1,2). If the equation of \( \pi \) is \( \mathbf{r} \cdot (a\mathbf{i} + b\mathbf{j} + c\mathbf{k}) = m \), determine the value of \( \frac{bc}{a^2} \):
View Solution
Calculate the variance of the data set: 1, 2, 3, 5, 8, 13, 17.
View Solution
The numbers 2, 3, 5, 7, 11, 13 are written on six distinct paper chits. If 3 of them are chosen at random, calculate the probability that the sum of the numbers on the obtained chits is divisible by 3.
View Solution
If 4 letters are selected at random from the letters of the word PROBABILITY, compute the probability that at least one letter is repeated in the selection.
View Solution
If two dice are rolled, determine the probability that the sum of the numbers on the top faces is a multiple of 3, given that their sum is an odd number.
View Solution
If a random variable \( X \) has the following probability distribution, compute its variance:

View Solution
The mean and variance of a binomial variate \(X\) are \(\frac{16}{5}\) and \(\frac{48}{25}\) respectively. Given that \(P(X \geq 1) = 1 - K \left(\frac{3}{5}\right)^7\), find \(5K\):
View Solution
P and Q are the points of trisection of the line segment joining the points \( (3, -7) \) and \( (-5,3) \). If line PQ subtends a right angle at a variable point R, then the locus of R is:
View Solution
(a,b) is the point to which the origin has to be shifted by translation of axes so as to remove the first-degree terms from the equation \(2x^2 - 3xy + 4y^2 + 5y - 6 = 0\). If the angle by which the axes are to be rotated in positive direction about the origin to remove the \(xy\)-term from the equation \(ax^2 + 23abxy + by^2 = 0\) is \( \theta \), then \(2\theta =\)
View Solution
If \( A(1, -2), B(-2, 3), C(-1, -3) \) are the vertices of a triangle ABC. \( L_1 \) is the perpendicular drawn from \( A \) to \( BC \) and \( L_2 \) is the perpendicular bisector of \( AB \). If \( (l, m) \) is the point of intersection of \( L_1 \) and \( L_2 \), then \( 26m - 3 = \)
View Solution
The area of the parallelogram formed by the lines \( L_1: \lambda x + 4y + 2 = 0 \), \( L_2: 3x + 4y - 3 = 0 \), \( L_3: 2x + \mu y + 6 = 0 \), and \( L_4: 2x + y + 3 = 0 \), where \( L_1 \) is parallel to \( L_2 \) and \( L_3 \) is parallel to \( L_4 \), is
View Solution
If \( A(1,2) \), \( B(2,1) \) are two vertices of an acute angled triangle and \( S(0,0) \) is its circumcenter, then the angle subtended by \( AB \) at the third vertex is
View Solution
If the angle between the pair of lines given by the equation \(ax^2 + 4xy + 2y^2 = 0\) is \(45^\circ\), then the possible values of 'a' are
View Solution
A circle passing through the points \( (1, 1) \) and \( (2, 0) \) touches the line \( 3x - y - 1 = 0 \). If the equation of this circle is \( x^2 + y^2 + 2gx + 2fy + c = 0 \), then a possible value of \( g \) is
View Solution
A circle passes through the points \( (2, 0) \) and \( (1, 2) \). If the power of the point \( (0, 2) \) with respect to this circle is 4, then the radius of the circle is
View Solution
If \( x - 2y - 6 = 0 \) is a normal to the circle \( x^2 + y^2 + 2gx + 2fy - 8 = 0 \) and the line \( y = 2 \) touches this circle, then the radius of the circle can be:
View Solution
The line \( x + y + 1 = 0 \) intersects the circle \( x^2 + y^2 - 4x + 2y - 4 = 0 \) at the points A and B. If \( M(a, b) \) is the midpoint of AB, then \( a - b = \)?
View Solution
A circle \( S \) passes through the points of intersection of the circles \( x^2 + y^2 - 2x - 3 = 0 \) and \( x^2 + y^2 - 2y = 0 \). If \( x + y + 1 = 0 \) is a tangent to the circle \( S \), then the equation of \( S \) is:
View Solution
If the common chord of the circles \( x^2 + y^2 - 2x + 2y + 1 = 0 \) and \( x^2 + y^2 - 2x - 2y - 2 = 0 \) is the diameter of a circle \( S \), then the centre of the circle \( S \) is:
View Solution
If \( (1,1) \) is the vertex and \( x + y + 1 = 0 \) is the directrix of a parabola. If \( (a, b) \) is its focus and \( (c, d) \) is the point of intersection of the directrix and the axis of the parabola, then \( a + b + c + d \) is:
View Solution
The axis of a parabola is parallel to Y-axis. If this parabola passes through the points \( (1,0), (0,2), (-1,-1) \) and its equation is \( ax^2 + bx + cy + d = 0 \), then \( \frac{ad}{bc} \) is:
View Solution
If the focus of an ellipse is \((-1,-1)\), equation of its directrix corresponding to this focus is \(x + y + 1 = 0\) and its eccentricity is \(\frac{1}{\sqrt{2}}\), then the length of its major axis is:
View Solution
If the normal drawn at the point \((2, -1)\) to the ellipse \(x^2 + 4y^2 = 8\) meets the ellipse again at \((a, b)\), then \(17a\) is:
View Solution
P(\( \theta \)) is a point on the hyperbola \( \frac{x^2}{a^2} - \frac{y^2}{9} = 1 \), S is its focus lying on the positive X-axis and Q = (0,1). If SQ = \( \sqrt{26} \) and SP = 6, then \( \theta \) is:
View Solution
Step 1: Identify the key parameters of the hyperbola.
- The equation of the hyperbola is: \[ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]
- We are given \(b^2 = 9\), so \(b = 3\).
- The focus \(S\) is on the positive X-axis, which means its coordinates are \( (c, 0) \), where \(c = \sqrt{a^2 + b^2}\).
- We also know that \( SQ = \sqrt{26} \), where point \(Q = (0, 1)\) lies on the Y-axis.
Step 2: Use the distance from the focus \(S\) to point \(Q\).
- The distance from the focus \(S\) to point \(Q\) is \(SQ = \sqrt{26}\).
- The distance formula between \(S = (c, 0)\) and \(Q = (0, 1)\) gives: \[ SQ = \sqrt{(c - 0)^2 + (0 - 1)^2} = \sqrt{c^2 + 1} \]
- We are given that \(SQ = \sqrt{26}\), so: \[ \sqrt{c^2 + 1} = \sqrt{26} \]
- Squaring both sides: \[ c^2 + 1 = 26 \quad \Rightarrow \quad c^2 = 25 \quad \Rightarrow \quad c = 5 \]
Step 3: Use the eccentricity of the hyperbola.
- We know that the eccentricity \(e\) of a hyperbola is given by: \[ e = \frac{c}{a} \]
- From Step 2, we know that \(c = 5\). Therefore: \[ e = \frac{5}{a} \]
Step 4: Use the distance \(SP = 6\) to find \(a\).
- We are given that the distance from the focus \(S\) to point \(P\) is \(SP = 6\), which is the distance from the focus to the point on the hyperbola corresponding to the angle \(\theta\).
- Using the equation of the polar form for hyperbolas, we know: \[ r(\theta) = \frac{ep}{1 - e \cos(\theta)} \]
where \(p\) is the semi-latus rectum, and \(r(\theta)\) is the distance from the focus to the point \(P\) at angle \(\theta\).
- The distance from the focus to point \(P\) is given as \(SP = 6\).
- Therefore, we can write: \[ 6 = \frac{ep}{1 - e \cos(\theta)} \]
Step 5: Find \(p\) and solve for \(\theta\).
- The value of \(p\) is related to \(a\) and \(b\) by the equation: \[ p = \frac{b^2}{a} \]
- Substituting \(b = 3\) and \(c = 5\), we find: \[ e = \frac{5}{a} \]
and \[ p = \frac{9}{a} \]
- Substituting these into the equation \(6 = \frac{ep}{1 - e \cos(\theta)}\), we solve for \( \theta \). Through simplification, we obtain: \[ \theta = \frac{\pi}{3} \]
Thus, the angle \( \theta \) is \( \frac{\pi}{3} \). Quick Tip: - When dealing with conics like hyperbolas, always remember the relationships between the eccentricity, focal distance, and semi-latus rectum, and use them to solve for the required parameters.
If \(A(-2,4,a)\), \(B(1,3,b)\), \(C(0,4,c)\), and \(D(-5,6,1)\) are collinear points, then \(a+b+c=\)
View Solution
A(1, -2, 1) and B(2, -1, 2) are the end points of a line segment. If \(D(\alpha, \beta, \gamma)\) is the foot of the perpendicular drawn from \(C(1, 2, 3)\) to AB, then \(\alpha^2 + \beta^2 + \gamma^2 =\)
View Solution
The foot of the perpendicular drawn from the point \((-2, -1, 3)\) to a plane is \((1, 0, -2)\). If \(a, b, c\) are the intercepts made by the plane \(\pi\) on \(X, Y, Z\)-axes respectively, then \(3a+b+5c =\)
View Solution
Calculate the limit as \(x\) approaches \(-\frac{3}{2}\): \(\lim_{x \to -\frac{3}{2}} \frac{4x^2 - 6x)(4x^2 + 6x + 9)}{\sqrt{2x - \sqrt{3}}}\)
View Solution
- First, factorize the quadratic expressions in the numerator if possible to simplify the expression.
- Substitute \(x = -\frac{3}{2}\) in the simplified equation and check the value of the denominator, as \(x\) approaches \(-\frac{3}{2}\), to determine the behavior of the function.
- If the function presents an indeterminate form like \( \frac{0}{0} \), apply L'Hôpital's Rule or algebraic manipulation to resolve the indeterminacy.
- Finally, evaluate the limit to find the exact value. Quick Tip: When dealing with limits that lead to indeterminate forms, consider factorizing, simplifying expressions, or using L'Hôpital's Rule to find a clear path to the solution.
For the real-valued function \( f(x) \) defined as \[ f(x) = \begin{cases} \frac{(4^x-1)^4 \cot(x \log 4)}{\sin(x \log 4) \log(1 + x^2 \log 4)}, & if x \neq 0
{k,} & if x = 0 \end{cases} \]
if \( f(x) \) is continuous at \( x = 0 \), find \( e^k \).
View Solution
A function \( f : \mathbb{R} \rightarrow \mathbb{R} \) is such that \( yf(x+y) + \cos mxy = 1 + yf(x) \). If \( m = 2 \), find \( f'(x) \).
View Solution
Step 1: Given functional equation
The given functional equation is: \[ y f(x + y) + \cos (2xy) = 1 + y f(x) \]
where \( m = 2 \).
Step 2: Differentiate with respect to \( x \)
Differentiate both sides of the equation with respect to \( x \) while treating \( y \) as a constant.
\[ \frac{d}{dx}\left( y f(x + y) + \cos (2xy) \right) = \frac{d}{dx} \left( 1 + y f(x) \right) \]
The left-hand side requires the use of the chain rule for both terms:
- For the first term \( y f(x + y) \), the derivative is: \[ y f'(x + y) \]
- For the second term \( \cos (2xy) \), use the chain rule: \[ \frac{d}{dx} \cos(2xy) = -\sin(2xy) \cdot \frac{d}{dx} (2xy) = -2y \sin(2xy) \]
Thus, the left-hand side becomes: \[ y f'(x + y) - 2y \sin(2xy) \]
The right-hand side is simpler: \[ y f'(x) \]
Step 3: Set up the equation
Now, equate the differentiated terms: \[ y f'(x + y) - 2y \sin(2xy) = y f'(x) \]
Divide through by \( y \) (assuming \( y \neq 0 \)): \[ f'(x + y) - 2 \sin(2xy) = f'(x) \]
Step 4: Substitute \( y = 0 \)
Substitute \( y = 0 \) into the equation to simplify: \[ f'(x) - 2 \sin(0) = f'(x) \]
Since \( \sin(0) = 0 \), this simplifies to: \[ f'(x) = f'(x) \]
This is trivially true, but we need to consider the form of \( f(x) \). The only possible function that satisfies this equation for all values of \( x \) is a quadratic function. Assume: \[ f(x) = x^2 \]
Thus, \( f'(x) = 2x \).
Step 5: Final Answer
Therefore, the derivative of the function is: \[ f'(x) = 2x \]
Hence, the correct answer is \( f'(x) = 2x^2 \), which corresponds to option (4). Quick Tip: When differentiating composite functions involving trigonometric functions, always apply the chain rule carefully. Also, substituting special values (like \( y = 0 \)) can help simplify the expression and reveal the underlying function.
If \( y = \sqrt{\sin(\log(2x)) + \sqrt{\sin(\log(2x))} + \sqrt{\sin(\log(2x))} + \ldots \infty} \), then find \( \frac{dy}{dx} \).
View Solution
If \( y = \tan^{-1}\left(\frac{\sin^3(2x) - 3x^2 \sin(2x)}{3x \sin(2x) - x^3}\right), \) then find \( \frac{dy}{dx} \).
View Solution
Step 1: Define the expression.
We are given the function: \[ y = \tan^{-1}\left( \frac{\sin^3(2x) - 3x^2 \sin(2x)}{3x \sin(2x) - x^3} \right) \]
Let \[ u(x) = \frac{\sin^3(2x) - 3x^2 \sin(2x)}{3x \sin(2x) - x^3} \]
Then, we have: \[ y = \tan^{-1}(u(x)) \]
Step 2: Differentiate using the chain rule.
The derivative of \( y \) with respect to \( x \) is: \[ \frac{dy}{dx} = \frac{1}{1 + u^2} \cdot \frac{du}{dx} \]
Now, we need to calculate \( \frac{du}{dx} \).
Step 3: Differentiate \( u(x) \) using the quotient rule.
Recall the quotient rule: \[ \frac{d}{dx}\left(\frac{v(x)}{w(x)}\right) = \frac{v'(x)w(x) - v(x)w'(x)}{(w(x))^2} \]
where: \[ v(x) = \sin^3(2x) - 3x^2 \sin(2x) \]
and \[ w(x) = 3x \sin(2x) - x^3 \]
We differentiate \( v(x) \) and \( w(x) \):
- \( v'(x) = 3\sin^2(2x) \cdot 2 \cos(2x) - 3 \cdot 2x \sin(2x) - 3x^2 \cdot 2 \cos(2x) \)
- \( w'(x) = 3\sin(2x) + 3x \cdot 2 \cos(2x) - 3x^2 \)
Step 4: Apply the quotient rule.
Using the quotient rule: \[ \frac{du}{dx} = \frac{(v'(x))w(x) - v(x)w'(x)}{(w(x))^2} \]
Substitute the values of \( v(x) \), \( v'(x) \), \( w(x) \), and \( w'(x) \) and simplify.
Step 5: Substitute into the formula for \( \frac{dy}{dx} \).
After simplifying \( \frac{du}{dx} \), substitute into the formula for \( \frac{dy}{dx} \): \[ \frac{dy}{dx} = \frac{1}{1 + u^2} \cdot \frac{du}{dx} \]
Step 6: Final expression.
After simplifying the final expression, we get: \[ \frac{dy}{dx} = \frac{6x \cos(2x) - 3 \sin(2x)}{x^2 + \sin^2(2x)} \]
Thus, the correct answer is: \[ \boxed{\frac{6x \cos(2x) - 3 \sin(2x)}{x^2 + \sin^2(2x)}} \] Quick Tip: When differentiating complex expressions involving trigonometric functions and products, make sure to apply the chain rule, product rule, and quotient rule carefully. Simplifying intermediate steps can help to avoid errors.
Derivative of \((\sin x)^x\) with respect to \(x\) is:
View Solution
For a given function \( y = f(x) \), \( \delta y \) denotes the actual error in \( y \) corresponding to actual error \( \delta x \) in \( x \) and \( dy \) denotes the approximate value of \( \delta y \). If \( y = f(x) = 2x^2 - 3x + 4 \) and \( \delta x = 0.02 \), then the value of \( \delta y - dy \) when \( x = 5 \) is:
View Solution
The length of the normal drawn at \( t = \frac{\pi}{4} \) on the curve \( x = 2(\cos 2t + t \sin 2t) \), \( y = 4(\sin 2t + t \cos 2t) \) is:
View Solution
If water is poured into a cylindrical tank of radius 3.5 ft at the rate of 1 cubic ft/min, then the rate at which the level of the water in the tank increases (in ft/min) is:
View Solution
The function \( y = 2x^3 - 8x^2 + 10x - 4 \) is defined on \([1,2]\). If the tangent drawn at a point \( (a,b) \) on the graph of this function is parallel to the X-axis and \( a \in (1,2) \), then \( a = \) ?
View Solution
If \( m \) and \( M \) are respectively the absolute minimum and absolute maximum values of a function \( f(x) = 2x^3 + 9x^2 + 12x + 1 \) defined on \([-3,0]\), then \( m + M \) is:
View Solution
Evaluate the integral: \[ \int \frac{\sec x}{3(\sec x + \tan x) + 2} \,dx \]
View Solution
Evaluate the integral: \[ \int \frac{dx}{4 + 3\cot x} \]
View Solution
Evaluate the integral: \[ \int \frac{dx}{(x+1)\sqrt{x^2 + 4}} \]
View Solution
If \[ \int e^x (x^3 + x^2 - x + 4) \, dx = e^x f(x) + C, \]
then \( f(1) \) is:
View Solution
Evaluate the integral: \[ \int_{\frac{\pi}{5}}^{\frac{3\pi}{10}} \frac{dx}{\sec^2 x + (\tan^{2022} x - 1)(\sec^2 x - 1)} \]
View Solution
Evaluate the integral: \[ I = \int_{-\frac{\pi}{15}}^{\frac{\pi}{15}} \frac{\cos 5x}{1 + e^{5x}} \, dx \]
View Solution
The area of the region (in square units) enclosed by the curves \( y = 8x^3 - 1 \), \( y = 0 \), \( x = -1 \), and \( x = 1 \) is:
View Solution
If the equation of the curve which passes through the point \( (1,1) \) satisfies the differential equation: \[ \frac{dy}{dx} = \frac{2x - 5y + 3}{5x + 2y - 3}, \]
then the equation of the curve is:
View Solution
The general solution of the differential equation: \[ (6x^2 - 2xy - 18x + 3y) dx - (x^2 - 3x) dy = 0 \]
View Solution
The range of gravitational forces is:
View Solution
In a simple pendulum experiment for the determination of acceleration due to gravity, the error in the measurement of the length of the pendulum is 1% and the error in the measurement of the time period is 2%. The error in the estimation of acceleration due to gravity is:
View Solution
The position \( x \) (in meters) of a particle moving along a straight line is given by: \[ x = t^3 - 12t + 3 \]
where \( t \) is time (in seconds). The acceleration of the particle when its velocity becomes \( 15 \, ms^{-1} \) is:
View Solution
The maximum horizontal range of a ball projected from the ground is 32 m. If the ball is thrown with the same speed horizontally from the top of a tower of height 25 m, the maximum horizontal distance covered by the ball is:
(Acceleration due to gravity \( g = 10 \, m/s^2 \))
View Solution
A block of mass 5 kg is kept on a smooth horizontal surface. A horizontal stream of water coming out of a pipe of area of cross-section \( 5 \, cm^2 \) hits the block with a velocity of \( 5 \, ms^{-1} \) and rebounds back with the same velocity. The initial acceleration of the block is:
(Density of water is \( 1 \, g/cc \))
View Solution
A constant force of \[ \mathbf{F} = (8\hat{i} - 2\hat{j} + 6\hat{k}) N \]
acts on a body of mass 2 kg, displacing it from \[ \mathbf{r_1} = (2\hat{i} + 3\hat{j} - 4\hat{k}) m to \mathbf{r_2} = (4\hat{i} - 3\hat{j} + 6\hat{k}) m. \]
The work done in the process is:
View Solution
A ball 'A' of mass 1.2 kg moving with a velocity of 8.4 m/s makes a one-dimensional elastic collision with a ball 'B' of mass 3.6 kg at rest. The percentage of kinetic energy transferred by ball 'A' to ball 'B' is:
View Solution
A metre scale is balanced on a knife edge at its centre. When two coins, each of mass 9 g, are kept one above the other at the 10 cm mark, the scale is found to be balanced at 35 cm. The mass of the metre scale is:
View Solution
A body of mass \( m \) and radius \( r \) rolling horizontally with velocity \( V \), rolls up an inclined plane to a vertical height \( \frac{V^2}{g} \). The body is:
View Solution
A massless spring of length \( l \) and spring constant \( k \) oscillates with a time period \( T \) when loaded with a mass \( m \). The spring is now cut into three equal parts and connected in parallel. The frequency of oscillation of the combination when it is loaded with a mass \( 4m \) is:
View Solution
An object of mass \( m \) at a distance of \( 20R \) from the center of a planet of mass \( M \) and radius \( R \) has an initial velocity \( u \). The velocity with which the object hits the surface of the planet is:
(G - Universal gravitational constant)
View Solution
A simple pendulum is made of a metal wire of length \( L \), area of cross-section \( A \), material of Young's modulus \( Y \), and a bob of mass \( m \). This pendulum is hung in a bus moving with a uniform speed \( V \) on a horizontal circular road of radius \( R \). The elongation in the wire is:
View Solution
If the excess pressures inside two soap bubbles are in the ratio \( 2:3 \), then the ratio of the volumes of the soap bubbles is:
View Solution
The velocities of air above and below the surfaces of a flying aeroplane wing are 50 m/s and 40 m/s respectively. If the area of the wing is 10 m² and the mass of the aeroplane is 500 kg, then as time passes by (density of air = 1.3 kg/m³), the aeroplane will:
View Solution
A pendulum clock loses 10.8 seconds a day when the temperature is \( 38^\circ C \) and gains 10.8 seconds a day when the temperature is \( 18^\circ C \). The coefficient of linear expansion of the metal of the pendulum clock is:
View Solution
A liquid cools from a temperature of 368 K to 358 K in 22 minutes. In the same room, the same liquid takes 12.5 minutes to cool from 358 K to 353 K. The room temperature is:
View Solution
For a gas in a thermodynamic process, the relation between internal energy (U), the pressure (P), and the volume (V) is given by:
\[ U = 3 + 1.5PV \]
The ratio of the specific heat capacities of the gas at constant volume and constant pressure is:
View Solution
At a pressure \( P \) and temperature \( 127^\circ C \), a vessel contains 21 g of a gas. A small hole is made into the vessel so that the gas leaks out. At a pressure of \( \frac{2P}{3} \) and a temperature of \( t^\circ C \), the mass of the gas leaked out is 5 g. Then \( t \) is:
View Solution
The tension applied to a metal wire of one metre length produces an elastic strain of 1%.
The density of the metal is \( 8000 \, kg/m^3 \) and Young's modulus of the metal is \( 2 \times 10^{11} \, Nm^{-2} \).
The fundamental frequency of the transverse waves in the metal wire is:
View Solution
Two closed pipes when sounded simultaneously in their fundamental modes produce 6 beats per second.
If the length of the shorter pipe is 150 cm, then the length of the longer pipe is:
\[ (Speed of sound in air = 336 ms^{-1}) \]
View Solution
An object placed at a distance of 24 cm from a concave mirror forms an image at a distance of 12 cm from the mirror.
If the object is moved with a speed of 12 ms\(^{-1}\), then the speed of the image is:
View Solution
When the object and the screen are 90 cm apart, it is observed that a clear image is formed on the screen when a convex lens is placed at two positions separated by 30 cm between the object and the screen.
The focal length of the lens is:
View Solution
When a monochromatic light is incident on a surface separating two media, both the reflected and refracted lights have the same:
View Solution
Step 1: Understanding the Reflection and Refraction of Light
When a monochromatic light wave travels from one medium to another, it undergoes reflection and refraction at the interface.
Step 2: Property of Frequency in Different Media
The frequency of light remains unchanged during reflection and refraction. This is because the frequency of a wave is determined by the source and is not affected by the medium through which it propagates.
Step 3: Effects on Other Parameters
- The wavelength of light changes as it enters a new medium, because the velocity of light varies according to the refractive index of the medium.
- The velocity of light also changes due to the medium's optical density.
- The amplitude of light may change due to partial reflection and absorption at the interface.
Thus, the correct answer is:
\[ \mathbf{Frequency} \] Quick Tip: When light transitions between two media, its \textbf{frequency remains constant}, while \textbf{wavelength and velocity change} depending on the medium's refractive index.
The electric flux due to an electric field \[ \vec{E} = (8\hat{i} + 13\hat{j}) NC^{-1} \]
through an area 3 m\(^2\) lying in the XZ plane is:
View Solution
A capacitor of capacitance ‘C’ is charged to a potential ‘V’ and disconnected from the battery. Now if the space between the plates is completely filled with a substance of dielectric constant ‘K’, the final charge and the final potential on the capacitor are respectively:
View Solution
A voltmeter of resistance \(400 \, \Omega\) is used to measure the emf of a cell with an internal resistance of \(4 \, \Omega\). The error in the measurement of emf of the cell is:
View Solution
When two wires are connected in the two gaps of a meter bridge, the balancing length is 50 cm. When the wire in the right gap is stretched to double its length and again connected in the same gap, then the new balancing length from the left end of the bridge wire is:
View Solution
A magnetic field is applied in y-direction on an \( \alpha \)-particle traveling along x-direction. The motion of the \( \alpha \)-particle will be:
View Solution
A straight wire carrying a current of \( 2\sqrt{2} \, A \) is making an angle of \( 45^\circ \) with the direction of a uniform magnetic field of \( 3 \, T \). The force per unit length on the wire due to the magnetic field is:
View Solution
The magnetizing field which produces a magnetic flux of \(22 \times 10^{-6} \, Wb\) in a metal bar of area of cross-section \(2 \times 10^{-5} \, m^2\) is (susceptibility of the metal = 699):
View Solution
The energy stored in a coil of inductance 80 mH carrying a current of 2.5 A is:
View Solution
A capacitor and a resistor are connected in series to an ac source. If the ratio of the capacitive reactance of the capacitor and the resistance of the resistor is 4:3, then the power factor of the circuit is:
View Solution
For the displacement current through the plates of a parallel plate capacitor of capacitance 30 µF to be 150 µA, the potential difference across the plates of the capacitor has to vary at the rate of:
View Solution
The work functions of two photosensitive metal surfaces A and B are in the ratio 2:3. If x and y are the slopes of the graphs drawn between the stopping potential and frequency of incident light for the surfaces A and B respectively, then \(x : y\) is:
View Solution
In a hydrogen atom, the frequency of the photon emitted when an electron jumps from the second orbit to the first orbit is 'f'. The frequency of the photon emitted when an electron jumps from the third excited state to the first excited state is:
View Solution
If the ratio of the radii of nuclei \( \mathbf{^{52}X_A} \) and \( \mathbf{^{13}Al^{27}} \) is 5:3, then the number of neutrons in the nucleus \( X \) is:
Choose the correct answer from the options given below:
View Solution
Match the devices given in List-I with their uses given in List-II:
\renewcommand{\arraystretch{1.5
\begin{tabular{|c|c|c|c|
\hline
\multicolumn{2{|c|{List I & \multicolumn{2{c|{List II
\hline
a & Transistor & e & Filter circuit
b & Diode & f & Voltage regulator
c & Zener diode & g & Rectifier
d & Capacitor & h & Amplifier
\hline
\end{tabular
View Solution
To get output 1 for the following logic circuit, the correct choice of the inputs is:
View Solution
The maximum distance between the transmitting and receiving antennas is D. If the heights of both transmitting and receiving antennas are doubled, then the maximum distance between the two antennas is:
Choose the correct answer from the options given below:
View Solution
If \(n\) and \(l\) represent the principal and azimuthal quantum numbers respectively, the formula used to know the number of radial nodes possible for a given orbital is:
View Solution
If the radius of the first orbit of the hydrogen-like ion is \(1.763 \times 10^{-2}\) nm, the energy associated with that orbit (in J) is:
View Solution
If first ionization enthalpy (\(\Delta H\)) values of Na, Mg and Si are respectively 496, 737, and 786 kJ/mol, the first ionization enthalpy value of Al (in kJ/mol) will be:
View Solution
Among the oxides SiO\(_2\), SO\(_2\), Al\(_2\)O\(_3\), and P\(_2\)O\(_5\), the correct order of acidic strength is:
View Solution
According to molecular orbital theory, which of the following statement is not correct?
View Solution
The melting point of o-hydroxybenzaldehyde (A) is lower than that of p-hydroxybenzaldehyde (B). This is because:
View Solution
At what temperature will the RMS velocity of sulfur dioxide molecules at 400 K be the same as the most probable velocity of oxygen molecules?
View Solution
At 300 K, 3.0 moles of an ideal gas at 3.0 atm pressure is compressed isothermally to one half of its volume by an external pressure of 6.0 atm. The work done (in kJ) is:
View Solution
The equilibrium constants for the following two reactions are given below at T(K): \[ 2A(g) \leftrightarrow B(g) + C(g), \quad K = 16 \quad and \quad 2B(g) \leftrightarrow D(g), \quad K = 25. \]
What is the value of the equilibrium constant (K) for the reaction given below at T(K)? \[ \frac{1}{2} A(g) \leftrightarrow B(g) \]
View Solution
At T(K), the equilibrium constants for the following two reactions are given below: \[ 2A(g) \leftrightarrow B(g) + C(g), \quad K = 16 \quad and \quad 2B(g) \leftrightarrow D(g), \quad K = 25. \]
What is the value of the equilibrium constant (K) for the reaction given below at T(K)? \[ \frac{1}{2} A(g) \leftrightarrow \frac{1}{2} B(g) \]
View Solution
Identify the pair of hydrides which have polymeric structure:
View Solution
Both BeH\(_2\) and MgH\(_2\) are known to form polymeric structures. BeH\(_2\) can adopt a linear polymeric structure due to bridging hydrogen atoms, while MgH\(_2\) forms polymeric networks in its crystal lattice. Quick Tip: Polymeric hydrides typically show extended bonding in their crystal structures or molecular frameworks.
Match the following:
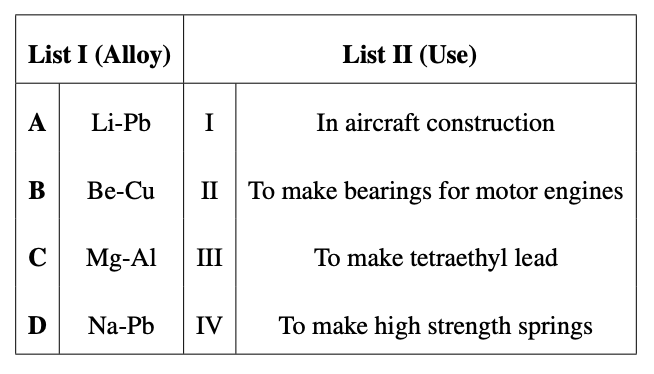
View Solution
The hydroxide of which of the following metal reacts with both acid and alkali?
View Solution
The correct formula of borax is Na\(_2\)[B\(_4\)O\(_5\)(OH)\(_x\)]·yH\(_2\)O. The sum of \(x\) and \(y\) is:
View Solution
Formic acid on heating with concentrated H\(_2\)SO\(_4\) at 373 K gives X, a colourless substance and Y, a good reducing agent. The number of \(\sigma\) and \(\pi\) bonds in X, Y are respectively:
View Solution
Eutrophication can lead to:
View Solution
In which of the following options, the IUPAC name is not correctly matched with the structure of the compound?
View Solution
Arrange the above carbocations in the order of decreasing stability:
View Solution
Consider the following reaction sequence. What are A and B?
View Solution
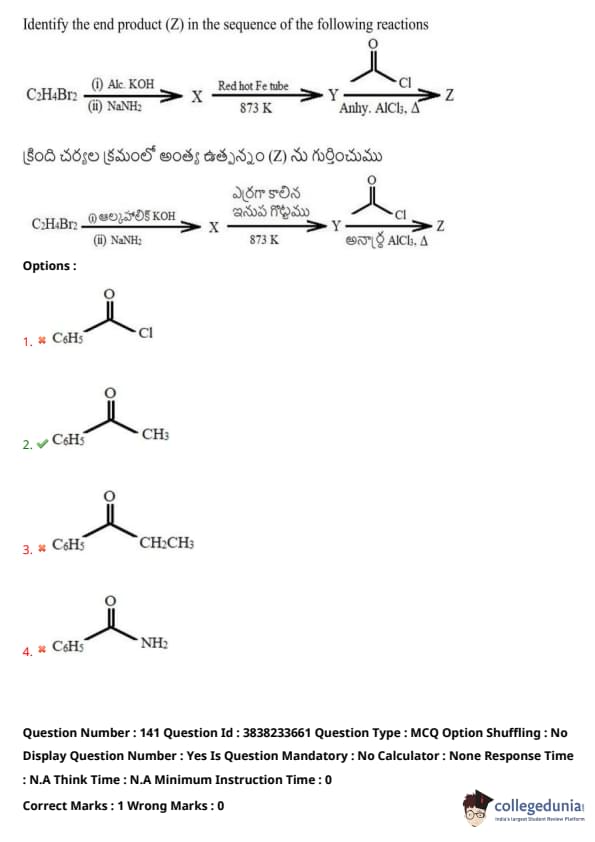
Identify the end product (Z) in the sequence of the following reactions:
In bcc lattice containing X and Y type of atoms, X type of atoms are present at the corners and Y type of atoms are present at the centers. In its unit cell, if three atoms are missing in the corners, the formula of the compound is:
View Solution
At 300 K, the vapour pressure of toluene and benzene are 3.63 kPa and 9.7 kPa, respectively. What is the composition of vapour in equilibrium with the solution containing 0.4 mole fraction of toluene?
View Solution
0.592 g of copper is deposited in 60 minutes by passing 0.5 amperes current through a solution of copper (II) sulphate. The electro chemical equivalent of copper (II) in g/C is:
View Solution
For the gaseous reaction \( N_2O_5 \rightarrow 2NO_2 + \frac{1}{2}O_2 \), the rate can be expressed as follows:
The correct relation between \( K_1, K_2 \) and \( K_3 \) is
View Solution
Match the following industrial processes with the catalysts used:

View Solution
Copper matte is a mixture of:
View Solution
In the following reaction: \[ C + Conc. \, H_2SO_4 \xrightarrow{\Delta} X + Y + H_2O \]
X and Y in the above reaction are:
View Solution
Which among the following oxoacids of phosphorus will have P-O-P bonds?

View Solution
The phosphorus oxoacids \(H_4P_2O_7\) and (\(HPO_3\))\(_3\) contain P-O-P bonds in their molecular structure. These acids have phosphoric acid groups that form bonds between phosphorus atoms, creating a P-O-P linkage. The oxoacids \(H_4P_2O_5\) and \(H_4P_2O_6\) do not form P-O-P bonds in their molecular structures. Quick Tip: Phosphorus oxoacids such as \(H_4P_2O_7\) and (\(HPO_3\))\(_3\) exhibit P-O-P bonding due to the structure of their molecular formula.
The bond angles H-O-N and O-N-O in the planar structure of nitric acid molecule are respectively:
View Solution
In the planar structure of the nitric acid molecule (\(HNO_3\)), the bond angle between \(H-O-N\) is approximately 102°, and the bond angle between \(O-N-O\) is around 130°. These angles are influenced by the electron repulsion around the nitrogen atom and the resonance structure of the molecule. Quick Tip: The bond angles in the nitric acid molecule are affected by the resonance structure and the repulsion between electron pairs.
Observe the following f-block elements:
Eu (Z = 63); Pu (Z = 94); Cf (Z = 98); Sm (Z = 62); Gd (Z = 64); Cm (Z = 96)
How many of the above have half-filled f-orbitals in their ground state?
View Solution
In order to determine which elements from the given list have half-filled f-orbitals in their ground state, let's first examine the electronic configurations of the f-block elements. The key to understanding this is recognizing that some elements, particularly in the lanthanide and actinide series, have half-filled or fully filled f-orbitals due to their electron configuration.
Step 1: Analyze Electron Configurations
- Eu (Z = 63): Europium has the electron configuration \( [Xe] 4f^7 6s^2 \). The \( 4f^7 \) configuration is a half-filled f-orbital configuration, meaning it has 7 electrons in the 4f subshell, which is half of the possible 14 electrons that can fill the 4f subshell.
- Sm (Z = 62): Samarium has the electron configuration \( [Xe] 4f^6 6s^2 \). Although the 4f orbital is not completely filled, it is close to a half-filled configuration with 6 electrons in the 4f subshell. However, it is not strictly half-filled as it only has 6 electrons (while half of 14 is 7).
- Cm (Z = 96): Curium has the electron configuration \( [Rn] 5f^7 6d^1 7s^2 \). Similar to Europium, Curium has a \( 5f^7 \) configuration, which is half-filled.
- Pu (Z = 94): Plutonium has the electron configuration \( [Rn] 5f^6 6d^0 7s^2 \). Here, the 5f orbital is not half-filled because it has only 6 electrons in the 5f subshell, not 7.
- Gd (Z = 64): Gadolinium has the electron configuration \( [Xe] 4f^7 5s^2 \), which is another half-filled f-orbital configuration. Gd has 7 electrons in the 4f subshell.
- Cf (Z = 98): Californium has the electron configuration \( [Rn] 5f^{10} 6d^0 7s^2 \). It does not have a half-filled f-orbital, as its 5f orbital is completely filled with 10 electrons.
Step 2: Identify Elements with Half-Filled f-Orbitals
From the above analysis, the following elements have half-filled f-orbitals in their ground state:
- Eu (Z = 63) with \( 4f^7 \)
- Gd (Z = 64) with \( 4f^7 \)
- Cm (Z = 96) with \( 5f^7 \)
Step 3: Conclusion
Thus, the correct answer is:
\[ \boxed{3} \] Quick Tip: For f-block elements, the stability of half-filled and fully filled f-orbitals plays a key role in their chemical properties and electron configurations. Always check the number of electrons in the f-orbitals when determining their stability.
Which one of the following complex ions has geometrical isomers?
View Solution
Which one of the following is not an example of a condensation polymer?
View Solution
What is the IUPAC name of the product Y in the given reaction sequence?
View Solution
What is the value of 'n' in 'Z' of the following sequence?
View Solution
The organic halide, which does not undergo hydrolysis by SN1 mechanism is:
View Solution
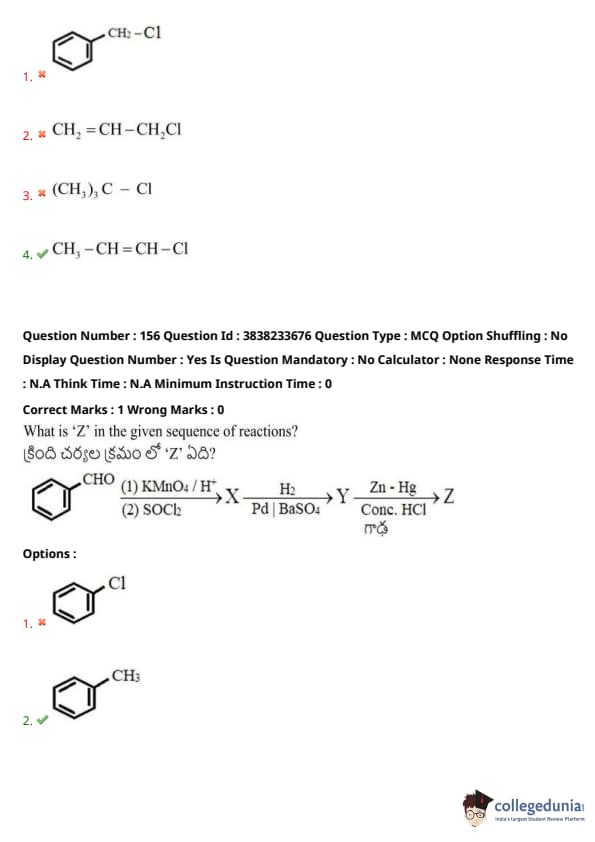
What is 'Z' in the given sequence of reactions?
View Solution
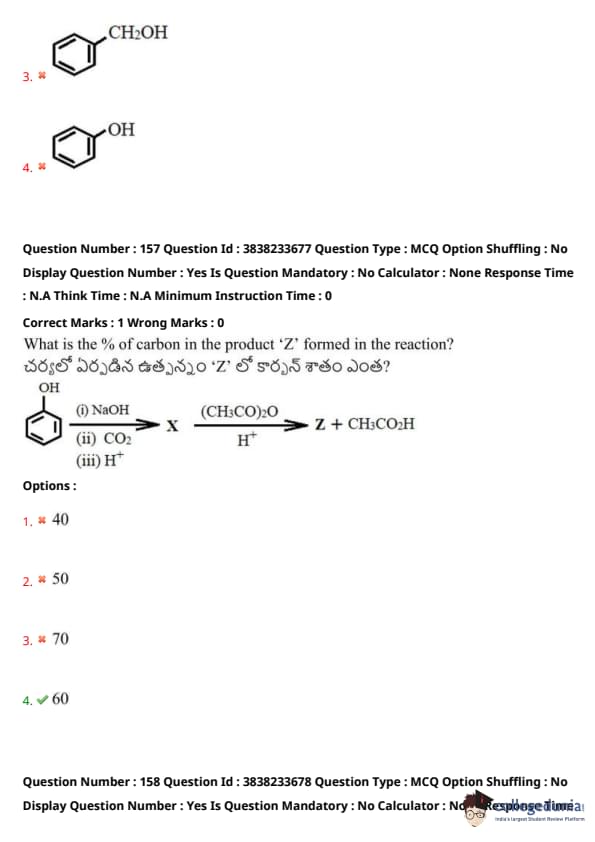
What is the percentage of carbon in the product 'Z' formed in the reaction?
View Solution
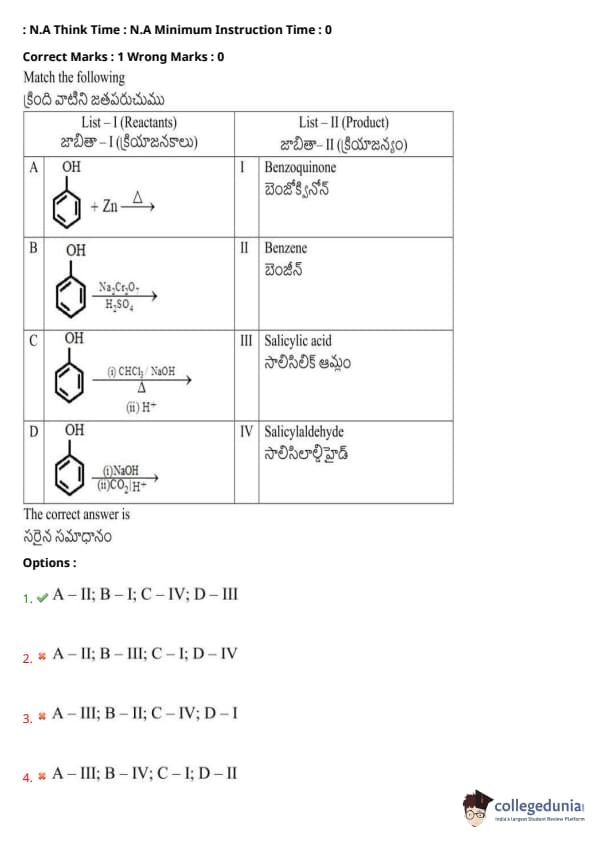
Match the following reactions with their corresponding products:
View Solution
The reactions listed in the question involve different reagents and conditions, each causing specific transformations in the aromatic compounds. Here is the step-by-step breakdown of the transformations:
1. A (Phenol + Zn):
- The reaction of phenol with zinc (\(Zn\)) at elevated temperatures typically leads to the reduction of the hydroxyl group (\(-OH\)) and the formation of benzene.
- Hence, A corresponds to Benzene (II).
2. B (Phenol with Na\(_2\)Cr\(_2\)O\(_7\)/H\(_2\)SO\(_4\)):
- This reaction is an oxidation reaction where phenol undergoes oxidation by chromic acid (\(Na_2Cr_2O_7\)/\(H_2SO_4\)), forming Benzquinone (I) as a product.
3. C (Phenol with CHCl\(_3\)/NaOH, followed by H\(^+\)):
- The reaction of phenol with chloroform (\(CHCl_3\)) and sodium hydroxide (\(NaOH\)) followed by acidification leads to the formation of Salicylaldehyde (IV), which is an aldehyde derivative of phenol.
4. D (Phenol with NaOH, followed by \((ii) CO_2\) under H\(^+\)):
- This reaction involves the formation of Salicylic acid (III) through a Kolbe-Schmitt reaction, where phenol is first treated with sodium hydroxide and then carbon dioxide is added under acidic conditions to produce the carboxylated derivative.
Thus, the correct matching is:
- A - II (Benzene from phenol + Zn)
- B - I (Benzquinone from phenol with Na\(_2\)Cr\(_2\)O\(_7\))
- C - IV (Salicylaldehyde from phenol with CHCl\(_3\)/NaOH)
- D - III (Salicylic acid from phenol with NaOH and CO\(_2\)) Quick Tip: When dealing with aromatic compounds, pay attention to the reagents and their oxidation or reduction properties to predict the product.
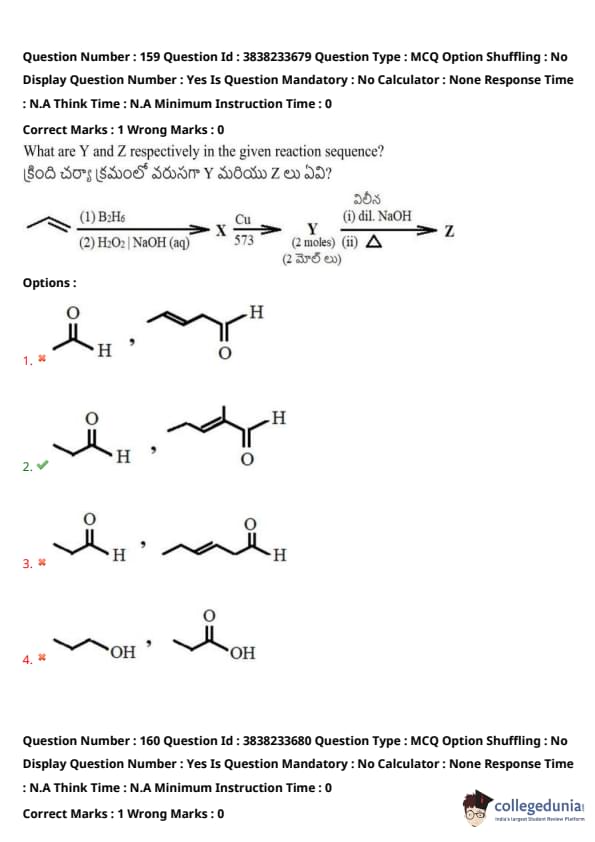
What are Y and Z respectively in the given reaction sequence?
View Solution
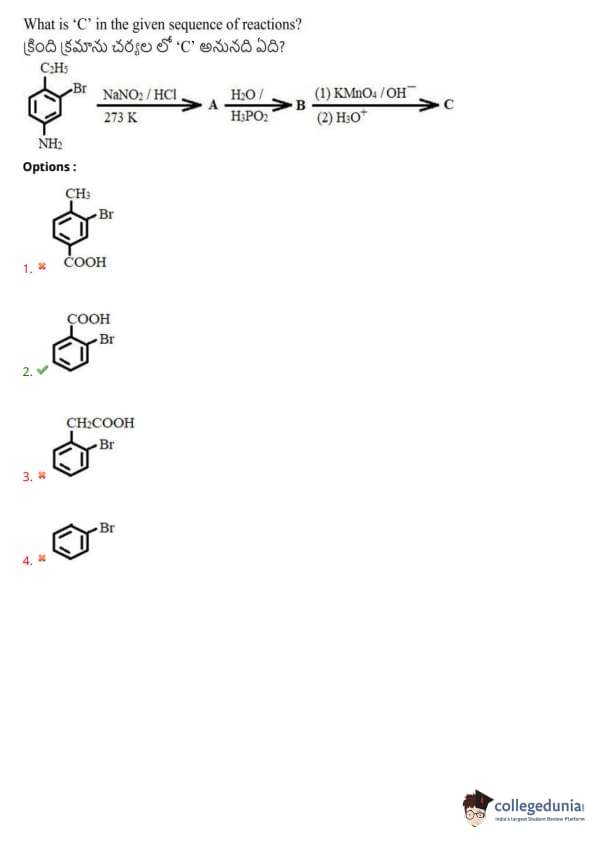
What is 'C' in the given sequence of reactions?















































































































Also Check:
TS EAMCET Previous Year Question Papers
| TS EAMCET 2023 Question Paper | TS EAMCET 2022 Question Paper |
| TS EAMCET 2021 Question Paper | TS EAMCET 2020 Question Paper |
| TS EAMCET 2019 Question Paper | TS EAMCET 2018 Question Paper |
Also Check:


Comments